Rationale and Objectives
We introduce a validation framework for the segmentation of brain tumors from magnetic resonance (MR) images. A novel unsupervised semiautomatic brain tumor segmentation algorithm is also presented.
Materials and Methods
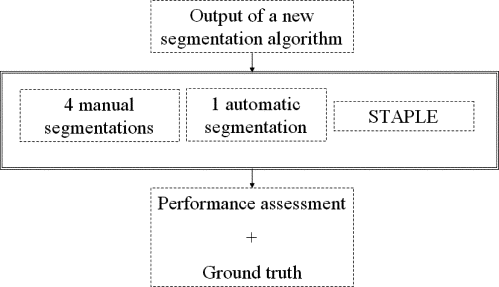
The proposed framework consists of 1) T1-weighted MR images of patients with brain tumors, 2) segmentation of brain tumors performed by four independent experts, 3) segmentation of brain tumors generated by a semiautomatic algorithm, and 4) a software tool that estimates the performance of segmentation algorithms.
Results
We demonstrate the validation of the novel segmentation algorithm within the proposed framework. We show its performance and compare it with existent segmentation. The image datasets and software are available at http://www.brain-tumor-repository.org/ .
Conclusions
We present an Internet resource that provides access to MR brain tumor image data and segmentation that can be openly used by the research community. Its purpose is to encourage the development and evaluation of segmentation methods by providing raw test and image data, human expert segmentation results, and methods for comparing segmentation results.
Brain tumor segmentation has long been recognized as a difficult problem. Many interactive and automated algorithms have been proposed for it for various types of clinical applications. It includes neurosurgery planning, radio- and chemotherapy monitoring and drug discovery. Some representative work can be found in ( ).
Despite the variety of methods published, there is no general algorithm accepted to segment brain tumors from magnetic resonance (MR) images. The reasons are manifold: 1) it is difficult to validate the segmentation algorithms due to intra- and interoperator variability in outlining the tumors; 2) the ground truth is often difficult to define; 3) the segmentation methods are tested on different image datasets; and 4) no common brain tumors database is available that enables standard benchmarking and comparison between various types of segmentation techniques; 5) no consensus exists on metrics to use for validation of segmentation algorithms; and 6) large datasets of MR brain tumor images are often not available for researchers that design segmentation algorithms.
Get Radiology Tree app to read full this article<
Materials and methods
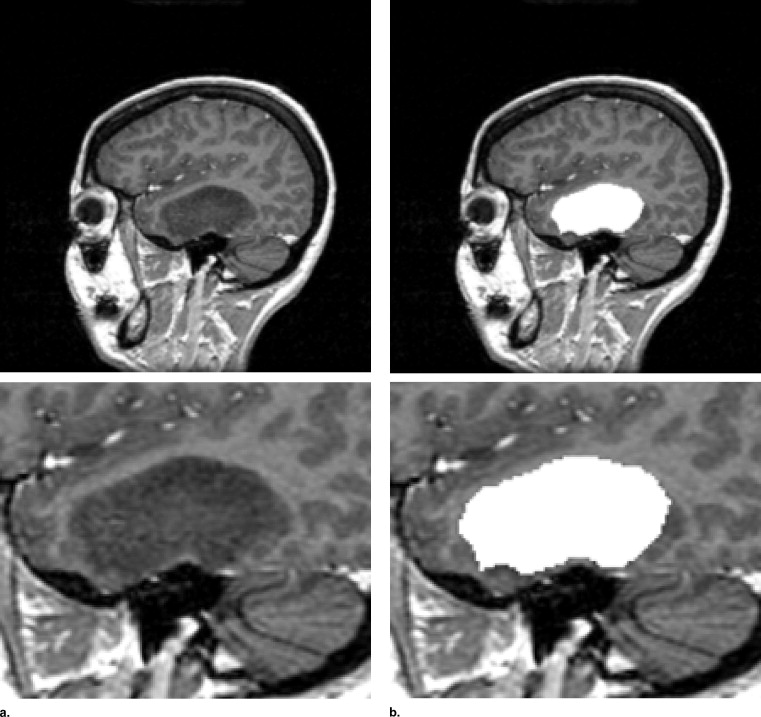
Brain Tumor Database
Get Radiology Tree app to read full this article<
Table 1
Details on the Current 10 Magnetic Resonance Imaging Datasets of Brain Tumors Proposed as Part of the Validation Framework
Patient Number Tumor Location 1 Meningioma Left frontal 2 Meningioma Left parasellar 3 Meningioma Right parietal 4 Low-grade glioma Left frontal 5 Astrocytoma Right frontal 6 Low-grade glioma Right frontal 7 Astrocytoma Right frontal 8 Astrocytoma Left temporal 9 Astrocytoma Left frontotemporal 10 Low-grade glioma Left temporal
Get Radiology Tree app to read full this article<
Existent Segmentation Data
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
The Performance Assessment of Image Segmentation Algorithms
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
A Novel Spectral Clustering Algorithm for Brain Tumor Segmentation
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
NCut(A,B)=cut(A,B)assoc(A,V)+cut(A,B)assoc(B,V). N
C
u
t
(
A
,
B
)
=
c
u
t
(
A
,
B
)
a
s
s
o
c
(
A
,
V
)
+
c
u
t
(
A
,
B
)
a
s
s
o
c
(
B
,
V
)
.
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Sij=⎧⎩⎨⎪⎪1−∥F(i)−F(j)∥2maxF−minF∥X(i)−X(j)∥20if∥X(i)−X(j)∥2<rotherwise⎫⎭⎬⎪⎪ S
i
j
=
{
1
−
∥
F
(
i
)
−
F
(
j
)
∥
2
m
a
x
F
−
m
i
n
F
∥
X
(
i
)
−
X
(
j
)
∥
2
i
f
∥
X
(
i
)
−
X
(
j
)
∥
2
<
r
0
o
t
h
e
r
w
i
s
e
}
where X ( i ) is the spatial location of node i , and F ( i ) is a feature vector, based on intensity. The values maxF and minF are, respectively, the maximum and the minimum values of F for the all the pixels in the image. Finally, the similarity matrix S is normalized by S = S/max ( S ) as proposed previously ( ). A requirement of NCut is the number of clusters. Overcoming this problem is a challenging task. Unsupervised clustering based solely on Fiedler eigenvector is a potential solution. In the unsupervised clustering, the user does not need to explicitly specify the number of clusters. More details follow.
Get Radiology Tree app to read full this article<
Fiedler Eigenvector for Unsupervised Image Segmentation
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Results
Get Radiology Tree app to read full this article<
Table 2
The STAPLE Output on for the 10 Datasets Used
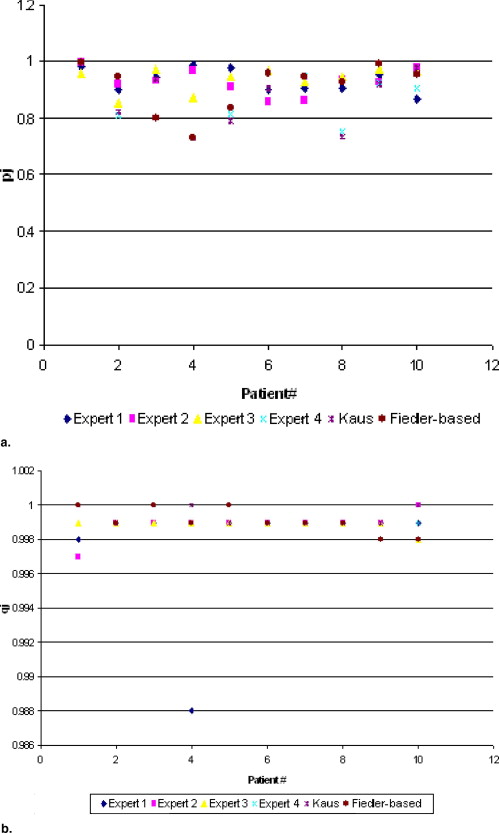
Expert 1 Expert 2 Expert 3 Expert 4 Kaus Novel Method (Fiedler based) Patient 1pj 0.986 1.000 0.959 1.000 1.000 1.000qj 0.998 0.997 0.999 1.000 1.000 1.000 Patient 2pj 0.899 0.920 0.857 0.809 0.822 0.947qj 0.999 0.999 0.999 0.999 0.999 0.999 Patient 3pj 0.945 0.933 0.977 0.936 0.936 0.798qj 0.999 0.999 0.999 1.000 1.000 1.000 Patient 4pj 0.988 0.970 0.875 0.733 0.733 0.733qj 0.988 0.999 0.999 1.000 1.000 0.999 Patient 5pj 0.981 0.910 0.949 0.813 0.793 0.837qj 0.999 0.999 0.999 0.999 0.999 1.000 Patient 6pj 0.899 0.858 0.968 0.907 0.905 0.960qj 0.999 0.999 0.999 0.999 0.999 0.999 Patient 7pj 0.904 0.864 0.929 0.951 0.946 0.947qj 0.999 0.999 0.999 0.999 0.999 0.999 Patient 8pj 0.907 0.938 0.946 0.753 0.736 0.931qj 0.999 0.999 0.999 0.999 0.999 0.999 Patient 9pj 0.955 0.930 0.975 0.922 0.918 0.993qj 0.999 0.999 0.999 0.999 0.999 0.998 Patient 10pj 0.867 0.978 0.971 0.908 0.978 0.956qj 0.999 1.000 0.998 0.999 1.000 0.998 Average_pj_ 0.9331 0.9301 0.9406 0.8732 0.8767 0.9102qj 0.9978 0.9989 0.9989 0.9993 0.9994 0.9991
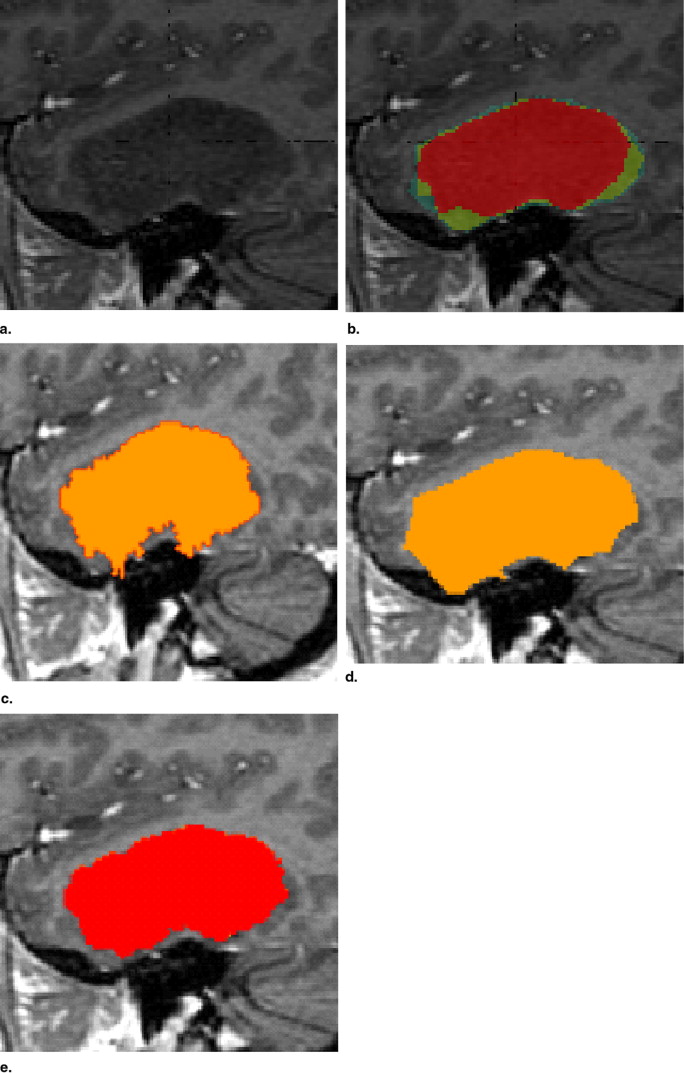
The segmentation of four experts, Kaus’ method, and a novel algorithm (Fiedler based) are used as input for simultaneous truth and performance level estimation. pj represent the true-positive fraction or sensitivity, while qj represent the true-negative fraction or specificity.
Get Radiology Tree app to read full this article<
Discussion and conclusions
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
References
1. Cates J.E., Whitaker R.T., Jones G.M.: Case study: an evaluation of user-assisted hierarchical watershed segmentation. Med Image Anal 2005; 9: pp. 566-578.
2. Cuadra M.B., Pollo C., Bardera A., et. al.: Atlas-based segmentation of pathological MR brain images using a model of lesion growth. IEEE Trans Med Imaging 2004; 23: pp. 1301-3014.
3. Droske M., Meyer B., Rumpf M., et. al.: An adaptive level set method for interactive segmentation of intracranial tumors. Neurol Res 2005; 27: pp. 363-370.
4. Kaus M.R., Warfield S.K., Nabavi A., et. al.: Automated segmentation of MR images of brain tumors. Radiology 2001; 218: pp. 586-591.
5. Letteboer M.M., Olsen O.F., Dam E.B., et. al.: Segmentation of tumors in magnetic resonance brain images using an interactive multiscale watershed algorithm. Acad Radiol 2004; 11: pp. 1125-1138.
6. Mazzara G.P., Velthuizen R.P., Pearlman J.L., et. al.: Brain tumor target volume determination for radiation treatment planning through automated MRI segmentation. Int J Radiat Oncol Biol Phys 2004; 59: pp. 300-312.
7. Vaidyanathan M., Clarke L.P., Hall L.O., et. al.: Monitoring brain tumor response to therapy using mri segmentation. Magn Res Imaging 1997; 15: pp. 323-334.
8. Xie K., Yang J., Zhang Z.G., et. al.: Semi-automated brain tumor and edema segmentation using MRI. Eur J Radiol 2005; 56: pp. 1.
9. Warfield S.K., Zou K.H., Wells W.M.: Simultaneous truth and performance level estimation (staple): an algorithm for the validation of image segmentation. IEEE Trans Med Imaging 2004; 23: pp. 72.
10. Shi J., Malik J.: Normalized cuts and image segmentation. IEEE Trans Pattern Anal Machine Intell 2000; 22: pp. 888-905.
11. Meila M., Shi J.: Learning segmentation by random walks.2000.pp. 873-879.
12. Archip N., Erard P.J., Egmont-Petersen M., et. al.: A knowledge-based approach for automatic detection of spinal cord in CT images. IEEE Trans Med Imaging 2002; 21: pp. 1504-1516.
13. Archip N., Rohling R., Cooperberg P., et. al.: Ultrasound image segmentation based on spectral clustering techniques. Ultrasound Med Biol 2005; 31: pp. 11.
14. Udupa J.K., Schmidt H., Leblanc V.R., et. al.: A framework for evaluating image segmentation algorithms. Comp Med Imaging Graph 2006; 30: pp. 1.