An Examination of Data Confidentiality and Disclosure Issues Related to Publication of Empirical ROC Curves

Rationale and Objectives

Grant funding institutions often require organizations to share their collected data as widely as possible while safeguarding the privacy of individuals. Summaries based on these data are often released. Here, the receiver operating characteristic (ROC) curve is explored for potential statistical disclosures in the presence of auxiliary data.

Materials and Methods

Formulas are introduced for calculating the missing data points from the full data set, given that a user has an empirical ROC curve and a subset of the data used to generate such a curve. Further, a discussion of the plausibility of this scenario is presented.

Results

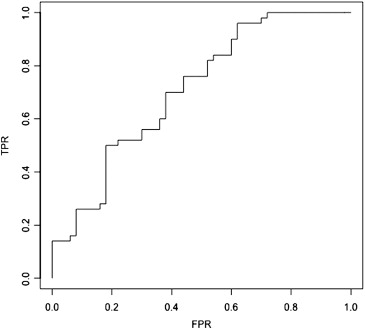
Diagnostic test data were simulated and an ROC curve was produced. Using a subset of the true data and the points on the empirical ROC curve, an attempt was made to reproduce the missing parts of the data. Disease statuses were able to be determined exactly, whereas test scores were solved for up to their rank.

Conclusions

If an individual or organization possessed the points of an empirical ROC curve and a subset of the true data, the true data underlying the ROC curve can be reproduced relatively accurately. As a result, the release of summaries of data, including the ROC curve, must be given careful thought before their release from a statistical disclosure perspective.

Many agencies that fund medical and public health research require that data collectors take precautions to protect the privacy of the individuals whose data are being collected . However, many of these same agencies also require data collectors to provide a plan to disseminate these collected data while still maintaining privacy . The first step in maintaining privacy of individual level data—referred to as microdata—that will be released for research is to remove obvious identifiers such as 18 identifiers outlined in the Health Insurance Portability and Accountability Act . These include information that could be easily used to identify an individual such as name, birth date, and social security number. However, simply removing these types of obvious identifiers is not enough to ensure individuals’ privacy. An example of this can be found in previous work , where the author was able to take deidentified public health data that was released to the public and combine these data with publicly available voting records in order to identify individuals in the released data. Therefore, although removing obvious identifiers is a necessary first step, it is certainly not sufficient to maintain the privacy of individuals.

Rationale and objectives

In general, there are a wide array of proposed methods for controlling statistical disclosure in microdata, for example, matrix masking and synthetic data . Although these methods, to some degree, add a layer of privacy to the data that will potentially be released, quantifying just how much protection these methods provide is another challenge. If a measure of privacy was established, data-releasing institutions could simply meet this privacy threshold before releasing data. However, there are many possible ways that disclosures can take place, and therefore many different proposals for how to quantify privacy. Linkage-based measures of privacy in which a malicious data user is trying to Identify a record in the data are presented elsewhere . Further proposals for assessing privacy can be found in the computer science literature . Measures of privacy based on inferential privacy include work on differential privacy and its variants as well as measures of privacy incorporating area under the receiver operating characteristic (ROC) curve .

Get Radiology Tree app to read full this article<

Materials and methods

Get Radiology Tree app to read full this article<

Plausibility

Get Radiology Tree app to read full this article<

Notation

Get Radiology Tree app to read full this article<

FPR(c)=FP(c)N⋆+(m−∑mj=1dXj)and F

(

)

(

)

⋆

(

−

∑

)

and

TPR(c)=TP(c)P⋆+∑mj=1dXj T

(

)

(

)

⋆

∑

where

FP(c)=∑n−mi=1(1−di)I(ti≥c)+∑mj=1(1−dXj)I(tXj≥c)TP(c)=∑n−mi=1diI(ti≥c)+∑mj=1dXjI(tXj≥c)I(ti>c)={10:ti≥c:ti<c F

(

)

∑

−

(

−

)

(

≥

)

∑

(

−

)

(

≥

)

(

)

∑

−

(

≥

)

∑

(

≥

)

(

)

{

≥

Get Radiology Tree app to read full this article<

Results

Example 1: One Missing Data Point

Get Radiology Tree app to read full this article<

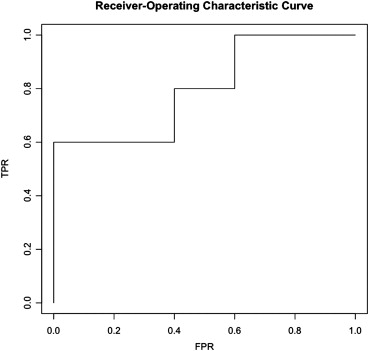
Table 1

Full Data, D , in the Two Left Columns, and a Subset of Data, D⋆ D

⋆ , in the Two Right Columns

Test Score Disease Status Test Score Disease Status 2.98 1 2.98 1 2.71 1 2.71 1 1.50 1 1.50 1 1.32 0 1.32 0 1.05 0 1.05 0tX1=0.61 t

0.61 dX1=1 d

1 0.53 0 0.53 0 0.51 1 0.51 1 −0.20 0 −0.20 0 −1.85 0 −1.85 0

Table 2

ROC Data

FPR TPR 0 0 0 0.2 0 0.4 0 0.6 0.2 0.6 0.4 0.6 0.4 0.8 0.6 0.8 0.6 1.0 0.8 1.0 1 1.0

Get Radiology Tree app to read full this article<

TPR(1.05)=3+dX1I(tX1≥1.05)4+dX1 T

(

1.05

)

(

≥

1.05

)

because P⋆=4 P

⋆

4 . This formula can be calculated for TPR and a similar formula calculated for FPR using each observed value of ti t

i as well as the unknown value of tX1 t

X as a cutoff.

Get Radiology Tree app to read full this article<

Example 2: More Than One Missing Data Point (m≥2) ( m ≥ 2 )

Get Radiology Tree app to read full this article<

Table 3

Results

Solution TruthtX t

X dX d

X tX t

X dX d

X 2.099 1 2.121 1 1.798 0 1.782 0 1.391 0 1.346 0 0.760 1 0.729 1 0.496 1 0.505 1 −0.096 1 −0.088 1 −0.610 1 −0.607 1 −0.813 1 −0.772 1 −6.686 0 −1.593 0 −8.978 0 −2.260 0

Get Radiology Tree app to read full this article<

Conclusions

Get Radiology Tree app to read full this article<

Acknowledgments

Get Radiology Tree app to read full this article<

Appendix

Description of the MCMC Procedure

Get Radiology Tree app to read full this article<

References

1. National Institutes of Health. NIH data sharing policy and implementation guidance. Available at: http://grants.nih.gov/grants/policy/data_sharing/data_sharing_guidance.htm . Accessed May 20, 2013.
2. National Science Foundation. Chapter II - proposal preparation instructions. Available at: http://www.nsf.gov/pubs/policydocs/pappguide/nsf11001/gpg_2.jsp . Accessed May 20, 2013.
3. National Institutes of Health. Final NIH statement on sharing research data. Available at: http://grants.nih.gov/grants/guide/notice-files/NOT-OD-03-032.html . Accessed May 20, 2013.
4. Chertoff J., Pisano E., Gert B.: Core curriculum: research ethics for radiology residents. Acad Radiol 2009; 16: pp. 108-116.
5. Health Insurance Portability and Accountability Act of 1996. Pub.L. 104-191, 110 Stat. 1936. Available at: http://www.gpo.gov/fdsys/pkg/PLAW-104publ191/html/PLAW-104publ191.htm . Accessed May 20, 2013.
6. Fetzer D., West O.: The HIPAA privacy rule and protected health information: implications in research involving DICOM image databases. Acad Radiol 2008; 15: pp. 390-395.
7. Avrin D.: HIPAA privacy and DICOM anonymization for research. Acad Radiol 2008; 15: pp. 273.
8. Sweeney L.: k-anonymity: a model for protecting privacy. Int J Uncertainty Fuzziness Knowledge Based Syst 2002; 10: pp. 557-570.
9. Cox L.H.: Matrix masking methods for disclosure limitation in microdata. Survey Methodol 1994; 6:: pp. 165-169.
10. Raghunathan T.E., Reiter J.P., Rubin D.B.: Multiple imputation for statistical disclosure limitation. J Official Stat 2003; 19: pp. 1-16.
11. Reiter J.P.: New approaches to data dissemination: a glimpse into the future (?). Chance 2004; 17: pp. 11-15.
12. Reiter J.P.: Releasing multiply imputed, synthetic public use microdata: an illustration and empirical study. J Roy Stat Soc Series A 2005; 168: pp. 185-205.
13. Matthews G.J., Harel O., Aseltine R.H.: Examining the robustness of fully synthetic data techniques for data with binary variables. J Stat Comput Simulation 2010; 80: pp. 609-624.
14. Paass G.: Disclosure risk and disclosure avoidance for microdata. J Business Econ Stat 1988; 6: pp. 487-500.
15. Duncan G., Lambert D.: The risk of disclosure for microdata. J Business Econ Stat 1989; 7: pp. 207-217.
16. Bethlehem J.G., Keller W., Pannekoek J.: Disclosure control of microdata. J Am Stat Assoc 1990; 85: pp. 38-45.
17. Marsh C., Skinner C., Arber S., et. al.: The case for samples of anonymized records from the 1991 census. J Royal Stat Soc 1991; 154: pp. 305-340.
18. Skinner C., Marsh C., Openshaw S., et. al.: Disclosure control for census microdata. J Official Stat 1994; 10: pp. 31-51.
19. Sweeney L.: Achieving k-anonymity privacy protection using generalization and suppression. Int J Uncertainty, Fuzziness and Knowledge Based Syst 2002; 10: pp. 571-588.
20. Machanavajjhala A., Kifer D., Gehrke J., et. al.: L-diversity: privacy beyond k-anonymity. ACM Trans Knowl Discov Data 2007; 1: pp. 3. http://doi.acm.org/10.1145/1217299.1217302
21. Li N, Li T, Venkatasubramanian S. t-closeness: privacy beyond k-anonymity and l-diversity. Data Engineering, 2007. ICDE 2007. IEEE 23rd International Conference. pp. 106–115.
22. Dwork C.: Differential privacy.ICALP.2006.Springerpp. 1-12.
23. Machanavajjhala A., Kifer D., Abowd J., et. al.: Privacy: theory meets practice on the map. International Conference on Data Engineering.2008.Cornell University Comuputer Science DepartmentCornell 10
24. Dwork C., Nissam K.: Privacy-preserving datamining on vertically partitioned databases. Adv Cryptol 2004; pp. 528-544.
25. Blum A, Dwork C, McSherry F, et al. Practical privacy: the sulq framework. Proceedings of the 24th ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, 2006; pp. 128–138.
26. Dwork C, Mcsherry F, Nissim K, et al. Calibrating noise to sensitivity in private data analysis. Proceedings of the 3rd Theory of Cryptography Conference. Springer, 2006; pp. 265–284.
27. Smith A. Efficient, differentially private point estimators. Available at: http://arxiv.org/abs/0809.4794. Accessed May 20, 2013.
28. Matthews G.J., Harel O., Aseltine R.H.: Assessing database privacy using the area under the receiver-operator characteristic curve. Health Serv Outcomes Res Methodol 2010; 10: pp. 1-15.
29. Matthews G., Harel O.: Assessing the privacy of randomized vector-valued queries to a database using the area under the receiver operating characteristic curve. Health Serv Outcomes Res Methodol 2012; 12: pp. 141-155.
30. Zou K.H., Liu A., Bandos A.I., et. al.: Statistical evaluation of diagnostic performance: topics in ROC analysis. Chapman and Hall/CRC Biostatistics Series 2011;
31. Pepe M.S.: The statistical evaluation of medical tests for classification and prediction.2003.Oxford University Press
32. Metz C.E.: Basic principles of ROC analysis. Semin Nucl Med 1978; 8: pp. 283-298.
33. Jha S.: Communicating results directly to patients: don’t ignore the price tag of this added value. Acad Radiol 2012; 19: pp. 643-645.
34. Kuhlman M., Meyer M., Krupinski E.: Direct reporting of results to patients: the future of radiology?. Acad Radiol 2012; 19: pp. 646-650.
35. Skinner C.: Statistical disclosure control for survey data.Pfeffermann D.Rao C.R.Handbook of statistics, vol. 29A: sample surveys: design, methods and applications.2009.pp. 381-396.
36. Matthews G.J., Harel O.: Data confidentiality: a review of methods for statistical disclosure limitation and methods for assessing privacy. Stat Surv 2011; 5: pp. 1-29.
37. Gelman A., Carlin J., Stern H., et. al.: Bayesian data analysis. Chapman Hall/CRC 2003;

An Examination of Data Confidentiality and Disclosure Issues Related to Publication of Empirical ROC Curves

Rationale and Objectives

Materials and Methods

Results

Conclusions

Rationale and objectives

Materials and methods

Plausibility

Notation

Results

Example 1: One Missing Data Point

Example 2: More Than One Missing Data Point (m≥2) ( m ≥ 2 )

Conclusions

Acknowledgments

Appendix

Description of the MCMC Procedure

References

Further Reading

A Brief History of Free-Response Receiver Operating Characteristic Paradigm Data Analysis

An Additive Selection of Markers to Improve Diagnostic Accuracy Based on a Discriminatory Measure

Estimating Sensitivity and Specificity for Technology Assessment Based on Observer Studies