Assessment of Performance Improvement in Content-based Medical Image Retrieval Schemes Using Fractal Dimension

Rationale and Objectives

The aim of this study was to investigate whether using a fractal dimension as an objective index (quantitative measure) to assess and control the “visual” or “texture” similarity of reference-image regions selected by a content-based image retrieval (CBIR) scheme would (or would not) affect the performance of the scheme in classification between image regions depicting suspicious breast masses.

Materials and Methods

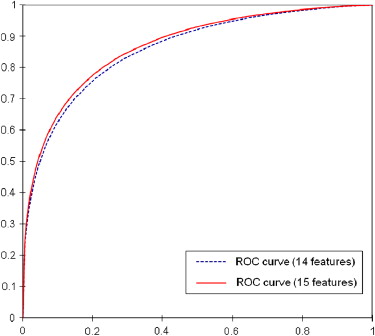
An image data set depicting 1500 verified mass regions and 1500 false-positive mass regions was used. Fourteen morphologic and intensity distribution features and a fractal dimension were computed. A CBIR scheme using a k -nearest neighbor classifier was applied, and two experiments were conducted. In the first experiment, the CBIR scheme was evaluated using all 15 features. In the second experiment, the fractal dimension was used as a prescreening feature to guide the CBIR scheme to search for the most similar reference images that had similar measures in the fractal dimension.

Results

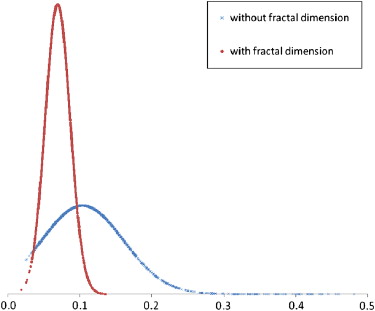
The CBIR scheme achieved classification performance with areas under the receiver-operating characteristic curve of 0.857 (95% confidence interval [CI], 0.844–0.870) using 14 features and 0.866 (95% CI, 0.853–0.879) after adding the fractal dimension ( P = .005 for both results). After using the fractal dimension as a prescreening feature, the CBIR scheme achieved an area under the receiver-operating characteristic curve of 0.851 (95% CI, 0.837–0.864), without a significant difference from the previous result using the original 14 features ( P = .120). The difference of fractal dimension values between the selected similar reference images was reduced by 56.7%, indicating improvement in image texture similarity. In addition, more than half of references were discarded early, without similarity comparisons, indicating improvement in searching efficiency.

Conclusions

This study demonstrated the feasibility of applying a fractal dimension as an objective (quantitative) and efficient search index to assess and maintain the texture similarity of reference mass regions selected by a CBIR scheme without reducing the scheme’s performance in classifying suspicious breast masses.

Content-based image retrieval (CBIR) schemes have been developed to search for images similar to a queried image from large reference-image databases on the basis of features or image content inherently contained within the images . In particular, the CBIR method has been proposed to overcome the difficulties encountered in textual annotation or description by manual methods for large image databases . Although the use of purely visual image querying is unlikely to be able to completely replace text-based searching methods, CBIR has the potential to be a very useful complement to text-based searching methods because of unique image characteristics . In the field of computer vision, CBIR has been one of the most active research areas over the past 30 years .

Currently, with the advances in digital technologies applied to medical imaging, a large number of diverse radiologic and pathologic images in digital format are rapidly produced in hospitals and medical centers using sophisticated image acquisition devices and digital scanners. These digital images have been routinely used for the purposes of diagnosis and therapy. The management of and access to these large image repositories has become increasingly complex and challenging . In reading and interpreting medical images in daily clinical practice, observers (ie, radiologists and pathologists) are often faced with new unknown and suspicious lesions, requiring them to search for and make comparisons to similar cases with previously verified results in their decision making in detection and diagnosis . This is a difficult and very time consuming task because of the rapid increase in the sizes of medical imaging databases. Therefore, developing and applying CBIR schemes to more effectively organize and retrieve images has attracted wide research interest in medical imaging and informatics . In particular, a number of studies have recently been conducted on how to develop and optimize CBIR schemes to search for similar breast lesions (including masses and microcalcification clusters) .

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Materials and methods

Reference-image Database

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Fractal Dimension

Get Radiology Tree app to read full this article<

P(u,v)=∣∣F(u,v)2∣∣=R(u,v)2+I(u,v)2, P

(

u

,

v

)

=

|

F

(

u

,

v

)

2

|

=

R

(

u

,

v

)

2

+

I

(

u

,

v

)

2

,

where u and v represent the horizontal and vertical components of frequencies, respectively, and R ( u , v ) and I ( u , v ) are the real and imaginary parts of the Fourier transform F ( u , v ), respectively. The power spectrum is displaced in polar form and shifted to locate zero frequency at the center. The scheme calculates log[ f ( u , v )], where f(u,v)=u2+v2−−−−−−√ f

(

u

,

v

)

=

u

2

+

v

2 , and average log[ P ( u , v )] in the condition of f(u,v)≤u2+v2−−−−−−√ f

(

u

,

v

)

≤

u

2

+

v

2 . Each set of u and v is defined by every 0.1 of log[ f ( u , v )] ( Fig 1 a). The slope of the curve on average log[ P ( u , v )] versus log[ f ( u , v )] is calculated by least-squares fitting ( Fig 1 b). Finally, the fractal dimension is calculated as

fractaldimension=(7−slope)/2. fractal

dimension

=

(

7

−

slope

)

/

2.

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

CBIR Scheme Using a k -Nearest Neighbor Classifier

Get Radiology Tree app to read full this article<

d(yT,xi)=∑FNr=1[fr(yT)−fr(xi)]2−−−−−−−−−−−−−−−−−−−√. d

(

y

T

,

x

i

)

=

∑

r

=

1

F

N

[

f

r

(

y

T

)

−

f

r

(

x

i

)

]

2

.

A smaller distance indicates a higher degree of “similarity” between two compared regions. The k NN classifier then computes a detection score to indicate the likelihood of being a true mass to the queried region:

PTP=∑Ni=1wTPi∑Ni=1wTPi+∑Mj=1wFPj,N+M=K, P

TP

=

∑

i

=

1

N

w

i

TP

∑

i

=

1

N

w

i

TP

+

∑

j

=

1

M

w

j

FP

,

N

+

M

=

K

,

where w i = 1/[ d ( y T , x i )] 2 (a distance weight), and wTPi w

i

TP and wFPj w

j

FP are the distance weights for the true-positive ( i ) and false-positive ( j ) mass regions, respectively. N is the number of verified true-positive mass regions, and M is the number of CAD-cued false-positive regions.

Get Radiology Tree app to read full this article<

Performance Evaluation

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Results

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Table 1

Performance of the Content-Based Image Retrieval Scheme and the Average Number of Early Discarded (Removed) Reference ROIs as a Function of the Comparison Threshold of the Fractal Dimension

α (Half of Difference Between Two Fractal Dimensions)A z 95% CI Average Number of Removed Reference ROIs 0.06 0.843 0.844–0.870 2140 0.07 0.843 0.829–0.857 1967 0.08 0.845 0.931–0.859 1835 0.09 0.850 0.836–0.862 1709 0.10 0.851 0.837–0.864 1588 0.20 0.853 0.839–0.866 695 0.30 0.853 0.839–0.865 272

A z , area under the receiver-operating characteristic curve; CI, confidence interval; ROI, region of interest.

Get Radiology Tree app to read full this article<

Discussion

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

References

• 1. Muller H., Michoux N., Bandon D., Geissbuhler A.: A review of content-based image retrieval systems in medical applications—clinical benefit and future direction. Int J Med Inform 2004; 73: pp. 1-23.

• 2. Lehmann T.M., Guld M.O., Deselaers T., et. al.: Automatic categorization of medical images for content-based retrieval and data mining. Comput Med Imaging Graph 2005; 29: pp. 143-155.

• 3. El-Naqa I., Yang Y., Galatsanos N.P., Wernick M.: A similarity learning approach to content based image retrieval: application to digital mammography. IEEE Trans Med Imaging 2004; 23: pp. 1233-1244.

• 4. Lam M.O., Disney T., Raicu D.S., Furst J., Channin D.S.: BRISC—an open source pulmonary nodule image retrieval framework. J Digit Imaging 2007; 20: pp. 63-77.

• 5. Smeulders A.M.W., Worring M., Santini S., Gupta A., Jain R.: Content-based image retrieval at the end of the early years. IEEE Trans Patt Anal Mach Intell 2000; 22: pp. 1349-1380.

• 6. Park S.C., Sukthankar R., Mummert L., Satyanarayanan M., Zheng B.: Optimization of reference library used in content-based medical image retrieval scheme. Med Phys 2007; 34: pp. 4331-4339.

• 7. Muramatsu C., Li Q., Suzuki K., et. al.: Investigation of psychophysical measures for evaluation of similar images for mammographic masses: preliminary results. Med Phys 2005; 32: pp. 2295-2304.

• 8. Karam O.H., Hamad A.M., Ghoniemy S., Rady S.: Enhancement of wavelet-based medical image retrieval through feature evaluation using an information gain measure.Proceedings of the Eighteenth Annual ACM Symposium on Applied Computing.2003.Association for Computing MachineryNew York:pp. 9-12.

• 9. Alto H., Rangayyan R.M., Desautels J.E.L.: Content-based retrieval and analysis of mammographic masses. J. Electron Imaging 2005; 14: pp. 1-17.

• 10. Wei C., Li C., Wilson R.: A general framework for content-based medical image retrieval with its application to mammograms. Proc SPIE 2005; 5748: pp. 134-143.

• 11. Muramatsu C., Li Q., Schmidt R.A., et. al.: Determination of subjective similarity for pairs of masses and pairs of clustered microcalcifications on mammograms: comparison of similarity ranking scores and absolute similarity ratings. Med Phys 2007; 34: pp. 2890-2895.

• 12. Zheng B., Lu A., Hardesty L.A., Gur D.: A method to improve visual similarity of breast masses for an interactive computer-aided diagnosis environment. Med Phys 2006; 33: pp. 111-117.

• 13. Wang X.H., Park S.C., Zheng B.: Improving performance of content-based image retrieval schemes in searching for similar breast mass regions: an assessment. Phys Med Biol 2009; 54: pp. 949-961.

• 14. Lefebvre F., Benali H., Gilles R., Kahn E., Paola R.D.: A Fractal approach to the segmentation of microcalcifications in digital mammograms. Med Phys 1995; 22: pp. 381-390.

• 15. Sedivy R., Windischberger C., Svozil K., Moser E., Breitenecker G.: Fractal analysis: an objective method for identifying atypical nuclei in dysplastic lesions of the cervix uteri. Gynecol Oncol 1999; 75: pp. 78-83.

• 16. Geraets W.G., van der Stelt P.F.: Fractal properties of bone. Dentomaxillofac Radiol 2000; 29: pp. 144-153.

• 17. Li H., Giger M.L., Olopade O.I., Lanm L.: Fractal analysis of mammographic parenchymal patterns in breast cancer risk assessment. Acad Radiol 2007; 4: pp. 513-521.

• 18. Hendee W.R.: Cognitive interpretation of visual signals.Hendee W.R.Wells P.N.T.The perception of visual information.1997.Springer-VerlagNew York:pp. 149-176.

• 19. Rangayyan R.M., Nguyen T.M.: Fractal analysis of contours of breast masses in mammograms. J Digit Imaging 2007; 20: pp. 223-237.

• 20. Xu C., Zhuang T.G., Hua Y.Q.: Discrimination of ground glass opacity on lung HRCT images using visual complexity measurements.Proceeding of the Second Joint EMBS/BMES Conference.2002.IEEENew York:pp. 1116-1117.

• 21. Peng F., Yu X., Xu G., Xia Q.: Fuzzy classification based on fractal features for undersea image. Int J Inform Technol 2005; 11: pp. 133-142.

• 22. Chevallet J.P., Maillot N., Lim J.H.: Concept propagation based on visual similarity application to medical image annotation. Third Asia Inform Retriev Symp 2006; 4182: pp. 514-521.

• 23. Soares F., Andruszkiewic P., Freire M.M., Cruz P., Pereira M.: Self-similarity analysis applied to 2D breast cancer imaging. Proc Int Conf Syst Network Commun 2007; 1: pp. 1-6.

• 24. Velanovich V.: Fractal analysis of mammographic lesions: a feasibility study quantifying the difference between benign and malignant masses. Am J Med Sci 1996; 311: pp. 211-214.

• 25. Byng J.W., Boyd N.F., Fishell E., Jong R.A., Yaffe M.J.: Automated analysis of mammographic densities. Phys Med Biol 1996; 41: pp. 909-923.

• 26. Chen J., Zheng B., Chang Y.H., Shaw C.C., Towers J.D., Gur D.: Fractal analysis of trabecular patterns in projection radiographs. An assessment. Invest Radiol 1994; 29: pp. 624-629.

• 27. Millard J., Augat P., Link T.M., et. al.: Power spectral analysis of vertebral trabecular bone structure from radiographs: orientation dependence and correlation with bone mineral density and mechanical properties. Calcifield Tissue Int 1998; 63: pp. 482-489.

• 28. Mitchell T.M.: Machine learning.1997.WCB/McGraw-HillBoston, MA

• 29. Zheng B., Abrams G., Britton C.A., et. al.: Evaluation of an interactive computer-aided diagnosis scheme for mammography: a pilot study. Proc SPIE 2007; 6515: 65151M-1–65151M-8

• 30. Felipe J.C., Traina C., Traina A.J.: A new family of distance functions for perceptual similarity retrieval of medical images. J Digit Imaging 2009; 22: pp. 183-201.

• 31. Zheng B., Abrams G., Leader J.K., et. al.: Agreement between ratings of mass spiculations by observers and a computer scheme. Proc SPIE 2007; 6514: 65141P-1–65141P-8