Rationale and Objectives
The aim of this study was to assess similarities and differences between methods of performance comparisons under binary (yes or no) and receiver-operating characteristic (ROC)–type pseudocontinuous (0–100) rating data ascertained during an observer performance study of interpretation of full-field digital mammography (FFDM) versus FFDM plus digital breast tomosynthesis.
Materials and Methods
Rating data consisted of ROC-type pseudocontinuous and binary ratings generated by eight radiologists evaluating 77 digital mammographic examinations. Overall performance levels were summarized with a conventionally used probability of correct discrimination or, equivalently, the area under the ROC curve (AUC), which under a binary scale is related to Youden’s index. Magnitudes of differences in the reader-averaged empirical AUCs between FFDM alone and FFDM plus digital breast tomosynthesis were compared in the context of fixed-reader and random-reader variability of the estimates.
Results
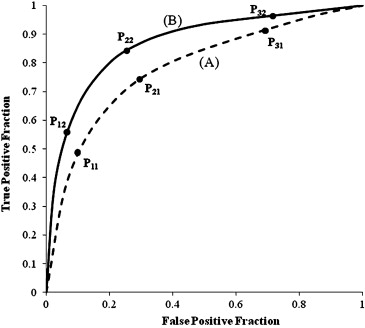
The absolute differences between modes using the empirical AUCs were larger on average for the binary scale (0.12 vs 0.07) and for the majority of individual readers (six of eight). Standardized differences were consistent with this finding (2.32 vs 1.63 on average). Reader-averaged differences in AUCs standardized by fixed-reader and random-reader variances were also smaller under the binary rating paradigm. The discrepancy between AUC differences depended on the location of the reader-specific binary operating points.
Conclusions
The human observer’s operating point should be a primary consideration in designing an observer performance study. Although in general, the ROC-type rating paradigm provides more detailed information on the characteristics of different modes, it does not reflect the actual operating point adopted by human observers. There are application-driven scenarios in which analysis based on binary responses may provide statistical advantages.
Performance assessments and comparisons of technologies and practices in radiology and other imaging-based fields require complicated, time-consuming, expensive studies, particularly when the observer is considered an integral part of the diagnostic system. Retrospective studies are frequently used for this purpose , but in recent years, prospective studies have also been used and have essentially become the gold standard for large, “pivotal” studies .
Regardless of the particular study design, rating data are often collected under a conventional receiver-operating characteristic (ROC)–type paradigm and are used to indicate the level of confidence in a particular noteworthy finding (or a suspected finding) in question. Whether the rating scale being used is discrete (eg, five categories) or pseudocontinuous (eg, 101 categories ranging from 0 to 100), and whether the data are collected for examinations as a whole (ROC) or for findings within examinations (free-response ROC or region-of-interest paradigms), ultimately, a decision threshold (explicit or latent) is used to obtain a “clinically relevant” performance characteristic (eg, sensitivity, specificity, predictive values).
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Methods
General Study Design
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Breast Findings
Get Radiology Tree app to read full this article<
Observers
Get Radiology Tree app to read full this article<
Performance of the Study
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Data Analysis
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Aˆ=∑n0i=1∑n1j=1ψ(xi,yj)n1n0ψ(xi,yj)=⎧⎩⎨⎪⎪00.51xi>yjxi=yjxi<yj, A
ˆ
=
∑
i
=
1
n
0
∑
j
=
1
n
1
ψ
(
x
i
,
y
j
)
n
1
n
0
ψ
(
x
i
,
y
j
)
=
{
0
0.5
1
x
i
y
j
x
i
=
y
j
x
i
<
y
j
,
where x i and y j are ratings for the actually negative and actually positive examinations, correspondingly. Under the binary scale, this index is equivalent to a linear scale transformation of a widely used Youden’s index :
Aˆ=∑n0i=1∑n1j=1ψ(xi,yj)n1n0=⎡⎣⎢xi,yj∈{0,1}]=12⎧⎩⎨⎪⎪1+∑n1j=1yjn1tpf−∑n0i=1xin0tpf⎫⎭⎬⎪⎪=1+Yˆ2. A
ˆ
=
∑
i
=
1
n
0
∑
j
=
1
n
1
ψ
(
x
i
,
y
j
)
n
1
n
0
=
[
x
i
,
y
j
∈
{
0
,
1
}
]
=
1
2
{
1
+
∑
j
=
1
n
1
y
j
n
1
︸
tpf
−
∑
i
=
1
n
0
x
i
n
0
︸
tpf
}
=
1
+
Y
ˆ
2
.
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Results
Get Radiology Tree app to read full this article<
Table 1
Comparison of the Two Modalities Under the Binary and Pseudocontinuous Derived Indices Using Probability of Correct Discrimination (AUC ∗ )
FPF TPF Binary Scale Pseudocontinuous Scale Reader FFDM Combination FFDM Combination FFDM Combination Difference_z_ FFDM Combination Difference_z_ 1 0.35 0.15 0.96 1.00 0.80 0.93 −0.12 −2.93 0.93 0.97 −0.04 −1.18 2 0.04 0.04 0.83 0.91 0.89 0.94 −0.04 −1.21 0.91 0.97 −0.06 −1.57 3 0.20 0.06 0.70 0.83 0.75 0.89 −0.14 −2.92 0.83 0.95 −0.12 −2.38 4 0.31 0.15 0.87 1.00 0.78 0.93 −0.15 −2.77 0.89 0.99 −0.10 −1.95 5 0.17 0.13 0.78 0.91 0.81 0.89 −0.08 −1.44 0.90 0.96 −0.06 −1.63 6 0.50 0.09 0.91 0.83 0.71 0.87 −0.16 −2.60 0.88 0.91 −0.02 −0.48 7 0.31 0.09 0.91 0.91 0.80 0.91 −0.11 −2.48 0.95 0.97 −0.02 −1.24 8 0.15 0.09 0.70 0.87 0.77 0.89 −0.11 −2.23 0.82 0.95 −0.13 −2.68 Overall 0.25 0.10 0.83 0.91 0.79 0.90 −0.12 −5.00 † 0.89 0.96 −0.07 −2.73 †
AUC, area under the curve; FFDM, full-field digital mammography; FPF, false-positive fraction; TPF, true-positive fraction.
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Discussion
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Conclusion
Get Radiology Tree app to read full this article<
Appendix
Get Radiology Tree app to read full this article<
2NRMSA(T)=2NR(n0+n1)MSpseudo(T)=(D¯¯¯RC)2, 2
N
R
M
S
A
(
T
)
=
2
N
R
(
n
0
+
n
1
)
M
S
p
s
e
u
d
o
(
T
)
=
(
D
¯
R
C
)
2
,
where N R is the number of readers, and
D¯¯¯RC=∑NRr=1DrCNR=∑NRr=1∑n0i=1∑n1j=1wrijNRn0n1=∑n0i=1∑n1j=1w¯¯¯∙ijn0n1=w¯¯¯∙∙∙ D
¯
R
C
=
∑
r
=
1
N
R
D
r
C
N
R
=
∑
r
=
1
N
R
∑
i
=
1
n
0
∑
j
=
1
n
1
w
r
i
j
N
R
n
0
n
1
=
∑
i
=
1
n
0
∑
j
=
1
n
1
w
¯
•
i
j
n
0
n
1
=
w
¯
•
•
•
and
DrC=A1rC−A2rC=∑n0i=1∑n1j=1ψ1rijn0n1−∑n0i=1∑NYj=1ψ2rijn0n1=∑n0i=1∑n1j=1wrijn0n1=w¯¯¯r∙∙wrij=ψ1rij−ψ2rij D
r
C
=
A
r
C
1
−
A
r
C
2
=
∑
i
=
1
n
0
∑
j
=
1
n
1
ψ
r
i
j
1
n
0
n
1
−
∑
i
=
1
n
0
∑
j
=
1
N
Y
ψ
r
i
j
2
n
0
n
1
=
∑
i
=
1
n
0
∑
j
=
1
n
1
w
r
i
j
n
0
n
1
=
w
¯
r
•
•
w
r
i
j
=
ψ
r
i
j
1
−
ψ
r
i
j
2
are the average ( D¯¯¯RC D
¯
R
C ) and reader-specific ( D rC ) differences in the empirical AUCs. This and the following equalities are based on a simple structure of the pseudovalues for the AUC difference:
D∼pseudocr=⎛⎝⎜⎜⎜⎜⎜⎜n0+n1−1n0−1w¯¯¯i∙r−n1n0−1w¯¯¯∙∙rifc≤n0(xisremoved)n0+n1−1n1−1w¯¯¯∙jr−n0n1−1w¯¯¯∙∙rifc>n0(yisremoved)⎞⎠⎟⎟⎟⎟⎟⎟⇒D˜¯¯¯pseudo∙∙=w¯¯¯∙∙∙ D
∼
c
r
p
s
e
u
d
o
=
n
0
+
n
1
−
1
n
0
−
1
w
¯
i
•
r
−
n
1
n
0
−
1
w
¯
•
•
r
if
c
≤
n
0
(
x
is
removed
)
n
0
+
n
1
−
1
n
1
−
1
w
¯
•
j
r
−
n
0
n
1
−
1
w
¯
•
•
r
if
c
n
0
(
y
is
removed
)
⇒
D
˜
¯
•
•
p
s
e
u
d
o
=
w
¯
•
•
•
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
2NR(n0+n1)MSpseudo(TC)=∑n0+n1c=1(D˜¯¯¯pseudoc∙−D˜¯¯¯pseudo∙∙)2(n0+n1)(n0+n1−1)=VˆJ1(D¯¯¯RC∣∣R), 2
N
R
(
n
0
+
n
1
)
M
S
p
s
e
u
d
o
(
T
C
)
=
∑
c
=
1
n
0
+
n
1
(
D
˜
¯
c
•
p
s
e
u
d
o
−
D
˜
¯
•
•
p
s
e
u
d
o
)
2
(
n
0
+
n
1
)
(
n
0
+
n
1
−
1
)
=
V
ˆ
J
1
(
D
¯
R
C
|
R
)
,
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
VˆJ1(D¯¯¯RC∣∣R)=[∑n0i=1(w¯¯¯i∙∙−w¯¯¯∙∙∙)2(n0−1)2+∑n1j=1(w¯¯¯∙j∙−w¯¯¯∙∙∙)2(n1−1)2]×n0+n1−1n0+n1. V
ˆ
J
1
(
D
¯
R
C
|
R
)
=
[
∑
i
=
1
n
0
(
w
¯
i
•
•
−
w
¯
•
•
•
)
2
(
n
0
−
1
)
2
+
∑
j
=
1
n
1
(
w
¯
•
j
•
−
w
¯
•
•
•
)
2
(
n
1
−
1
)
2
]
×
n
0
+
n
1
−
1
n
0
+
n
1
.
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
2NR[MSA(TR)+NR(CovJ1(AmrC,AmsC)¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯−CovJ1(A1rC,A2sC)¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯)]=1NR−1vˆBr+NRNR−1VˆJ1(D¯¯¯∣∣RCR)−1NR−1VˆJ1(DrC|r)¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯=VˆJ1(D¯¯¯RC) 2
N
R
[
M
S
A
(
T
R
)
+
N
R
(
Cov
J
1
(
A
r
C
m
,
A
s
C
m
)
¯
−
Cov
J
1
(
A
r
C
1
,
A
s
C
2
)
¯
)
]
=
1
N
R
−
1
v
ˆ
r
B
+
N
R
N
R
−
1
V
ˆ
J
1
(
D
¯
|
R
C
R
)
−
1
N
R
−
1
V
ˆ
J
1
(
D
r
C
|
r
)
¯
=
V
ˆ
J
1
(
D
¯
R
C
)
where vˆBr=2(NR−1)NR×MSA(TR)=∑NRr=1(DrC−D¯¯¯RC)2NR v
ˆ
r
B
=
2
(
N
R
−
1
)
N
R
×
M
S
A
(
T
R
)
=
∑
r
=
1
N
R
(
D
r
C
−
D
¯
R
C
)
2
N
R is a sample variability of the reader-specific differences in AUCs, VˆJ1(D¯¯¯RC∣∣R) V
ˆ
J
1
(
D
¯
R
C
|
R
) is a one-sample jackknife variance of the average difference, and VˆJ1(DrC|r)¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ V
ˆ
J
1
(
D
r
C
|
r
)
¯ is the average of N R reader-specific variance of differences. The jackknife variance for an individual reader can be obtained from equation A 1 by replacing w¯¯¯i∙∙ w
¯
i
•
• , w¯¯¯∙j∙ w
¯
•
j
• , and w¯¯¯∙∙∙ w
¯
•
•
• with w¯¯¯i∙r w
¯
i
•
r , w¯¯¯∙jr w
¯
•
j
r , and w¯¯¯∙∙r w
¯
•
•
r correspondingly. The last equality follows representation of the random-reader variance as a combination of the variance components .
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
MSpseudo(T)MSpseudo(TC)−−−−−−−−−√=D¯¯¯RCVˆJ1(D¯¯¯RC∣∣R)√ M
S
p
s
e
u
d
o
(
T
)
M
S
p
s
e
u
d
o
(
T
C
)
=
D
¯
R
C
V
ˆ
J
1
(
D
¯
R
C
|
R
)
or
MSA(T)MSA(TR)+NR(CovJ12−CovJ13)−−−−−−−−−−−−−−−−−−√=D¯¯¯RCVˆJ1(D¯¯¯RC)√ M
S
A
(
T
)
M
S
A
(
T
R
)
+
N
R
(
Cov
2
J
1
−
Cov
3
J
1
)
=
D
¯
R
C
V
ˆ
J
1
(
D
¯
R
C
)
for the fixed-reader and random-reader inferences, correspondingly. As conventional in analysis of variance methodology, under the DBM approach, the statistical significance of the z statistics is assessed using an F (Snedecor’s) distribution with specific degrees of freedom rather than the standard normal distribution.
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
References
1. Fenton J.J., Taplin S.H., Carney P.A., et. al.: Influence of computer-aided detection on performance of screening mammography. N Engl J Med 2007; 356: pp. 1399-1409.
2. Awai K., Murao K., Ozawa A., et. al.: Pulmonary nodules: estimation of malignancy at thin-section helical CT—effect of computer-aided diagnosis on performance of radiologists. Radiology 2006; 239: pp. 276-284.
3. Gur D., Sumkin J.H., Rockette H.E., et. al.: Changes in breast cancer detection and mammography recall rates after the introduction of a computer-aided detection system. J Natl Cancer Inst 2004; 96: pp. 185-190.
4. Andriole G.L., Crawford E.D., Grubb R.L., et. al.: PLCO Project Team. Mortality results from a randomized prostate-cancer screening trial. [published erratum appears in N Engl J Med 2009; 360:1797] N Engl J Med 2009; 360: pp. 1310-1319.
5. Pisano E.D., Gatsonis C., Hendrick E., et. al.: Digital Mammographic Imaging Screening Trial (DMIST) Investigators Group. Diagnostic performance of digital versus film mammography for breast-cancer screening. [published erratum appears in N Engl J Med 2006; 355:1840] N Engl J Med 2005; 353: pp. 1773-1783.
6. Clark K.W., Gierada D.S., Marquez G., et. al.: Collecting 48,000 CT exams for the lung screening study of the National Lung Screening Trial. J Digit Imaging 2009; 22: pp. 667-680.
7. Lehman C.D., Gatsonis C., Kuhl C.K., et. al.: ACRIN Trial 6667 Investigators Group. MRI evaluation of the contralateral breast in women with recently diagnosed breast cancer. N Engl J Med 2007; 356: pp. 1295-1303.
8. Rockette H.E., Gur D., Metz C.E.: The use of continuous and discrete confidence judgments in receiver operating characteristic studies of diagnostic imaging techniques. Invest Radiol 1992; 27: pp. 169-172.
9. Berbaum K.S., Dorfman D.D., Franken E.A., et. al.: An empirical comparison of discrete ratings and subjective probability ratings. Acad Radiol 2002; 9: pp. 756-763.
10. Gur D., Bandos A.I., Cohen C.S., et. al.: The “laboratory” effect: comparing radiologists’ performance and variability during prospective clinical and laboratory mammography interpretations. Radiology 2008; 249: pp. 47-53.
11. Berbaum K.S., Franken E.A., Dorfman D.D., et. al.: Satisfaction of search in diagnostic radiology. Invest Radiol 1990; 25: pp. 133-140.
12. Egglin T.K.P., Feinstein A.R.: Context bias: a problem in diagnostic radiology. JAMA 1996; 276: pp. 1752-1755.
13. Gur D., Bandos A.I., Fuhrman C.R., et. al.: The prevalence effect in laboratory environment: changing the confidence ratings. Acad Radiol 2007; 14: pp. 49-53.
14. Zhou X.H., Obuchowski N.A., McClish D.K.: Statistical methods in diagnostic medicine.2002.John WileyNew York
15. Gur D., Abrams G.S., Chough D.M., et. al.: Digital breast tomosynthesis: observer performance study. AJR Am J Roentgenol 2009; 193: pp. 586-591.
16. Good W.F., Abrams G.S., Catullo V.J., et. al.: Digital breast tomosynthesis: a pilot observer study. AJR Am J Roentgenol 2008; 190: pp. 865-869.
17. Hanley J.A., McNeil B.J.: The meaning and use of the area under receiver operating characteristic (ROC) curve. Radiology 1982; 143: pp. 29-36.
18. Hilden J., Glasziou P.: Regret graphs, diagnostic uncertainty and Youden’s index. Stat Med 1996; 15: pp. 969-986.
19. Dorfman D.D., Berbaum K.S., Metz C.E.: Receiver operating characteristic rating analysis: generalization to the population of readers and patients with the jackknife method. Invest Radiol 1992; 27: pp. 723-731.
20. Gur D., Rockette H.E., Bandos A.I.: “Binary” and “non-binary” detection tasks: are current performance measures optimal?. Acad Radiol 2007; 14: pp. 871-876.
21. Gur D., Bandos A.I., Klym A.H., et. al.: Agreement of the order of overall performance levels under different reading paradigms. Acad Radiol 2008; 15: pp. 1567-1573.
22. Gallas B., Bandos A.I., Samuelson F., et. al.: A framework for random-effects ROC analysis: biases with the bootstrap and other variance estimators. Comm Stat Theory Meth 2009; 38: pp. 2586-2603.
23. Obuchowski N.A., Rockette H.E.: Hypothesis testing of the diagnostic accuracy for multiple diagnostic tests: an ANOVA approach with dependent observations. Comm Stat Simul Comput 1995; 24: pp. 285-308.
24. Hillis S.L., Obuchowski N.A., Schartz K.M., et. al.: A comparison of the Dorfman-Berbaum-Metz and Obuchowski-Rockette methods for receiver operating characteristic (ROC) data. Stat Med 2005; 24: pp. 1579-1607.
25. Bandos AI, Rockette HE, Gur D. Resampling methods for the area under the ROC curve. Proceedings of the ICML 2006 workshop on ROC Analysis in Machine Learning, Pittsburgh, USA; 2006, pp.1-8.
26. Bandos A.I., Rockette H.E., Gur D.: Exact bootstrap variances of the area under the ROC curve. Comm Stat Theory Meth 2007; 36: pp. 2443-2461.