Multivariate Analysis of Structural and Diffusion Imaging in Traumatic Brain Injury

Rationale and Objectives

Diffusion tensor (DT) and T1 structural magnetic resonance images provide unique and complementary tools for quantifying the living brain. We leverage both modalities in a diffeomorphic normalization method that unifies analysis of clinical datasets in a consistent and inherently multivariate (MV) statistical framework. We use this technique to study MV effects of traumatic brain injury (TBI).

Materials and Methods

We contrast T1 and DT image-based measurements in the thalamus and hippocampus of 12 TBI survivors and nine matched controls normalized to a combined DT and T1 template space. The normalization method uses maps that are topology-preserving and unbiased. Normalization is based on the full tensor of information at each voxel and, simultaneously, the similarity between high-resolution features derived from T1 data. The technique is termed symmetric normalization for MV neuroanatomy (SyNMN). Voxel-wise MV statistics on the local volume and mean diffusion are assessed with Hotelling’s T__2 test with correction for multiple comparisons.

Results

TBI significantly (false discovery rate P < .05) reduces volume and increases mean diffusion at coincident locations in the mediodorsal thalamus and anterior hippocampus.

Conclusions

SyNMN reveals evidence that TBI compromises the limbic system. This TBI morphometry study and an additional performance evaluation contrasting SyNMN with other methods suggest that the DT component may aid normalization quality.

Traumatic brain injury (TBI) is the most frequent cause of death and disability in individuals ages 15–24 and is also prevalent in older adults ( ). TBI, most commonly caused by automotive accidents and falls, occurs at a rate of approximately 1 in 600 per year in the general population ( ), whereas up to 10% of soldiers returning from Iraq may suffer from some form of TBI ( ). Even mild TBI may lead to significant behavioral changes ( ) and is very likely to be under-reported, particularly by those who have experienced concussion ( ). In consequence, up to 2% of individuals in the United States live with TBI-related disability. Thus, focus on TBI as a public health concern is increasing, along with further development of sensitive tools for assessing axonal and cortical injury ( ), tracking recovery from these injuries ( ) and predicting outcome ( ).

Traditional T1 imaging may be used to uncover in vivo effects of TBI in the cortex and deep gray matter structures. Neuronal atrophy, from concussion, was detected with T1 imaging and linked to ongoing depression ( ), whereas TBI-related reductions in gray matter concentration have also been correlated with attention deficits ( ). Hippocampal volume may be reduced by TBI ( ), along with the basal forebrain ( ). The thalamus appears to undergo injury during or after TBI as assessed postmortem ( ), through finite element models of TBI ( ) and through large-deformation tensor-based morphometry of control and subject populations ( ). An additional postmortem report has indicated involvement of the mediodorsal thalamus, which has connections to the prefrontal cortex ( ). This finding has also been validated at the cellular level through neuropathology ( ) and through histochemical staining and explicit neuronal counts ( ). TBI effects in the hippocampus have also been verified neuropathologically ( ).

Get Radiology Tree app to read full this article<

Open full size image

Figure 1

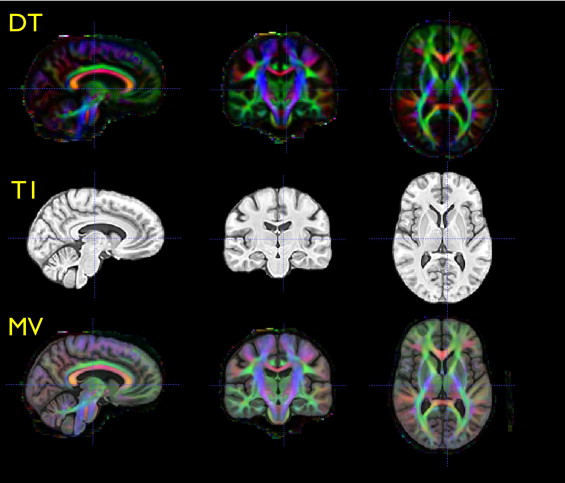
An overview of the steps required in our multivariate processing for population analysis of tensor and scalar components. The Jacobian measures local volume of neuroanatomy, whereas tensor-derived scalars relate to the integrity of cellular structure. Multivariate tests enable relationships between these variables to enhance statistical power for detecting group differences.

Get Radiology Tree app to read full this article<

Materials and methods

Get Radiology Tree app to read full this article<

Theory for Multivariate Image Processing

Multivariate datasets

Get Radiology Tree app to read full this article<

$Figure 2, Here we see one slice from the template T1 ( left ) and T1 plus diffusion tensor (DT) ( right ) after intramodality distortion correction. The RGB channel intensity is weighted by the fractional anisotropy (FA) and indicates principal fiber direction going left-to-right ( red ), going bottom-to-top ( green ), and going in-and-out of the page ( blue ) which are superimposed on the T1 image in the right panel .$

Get Radiology Tree app to read full this article<

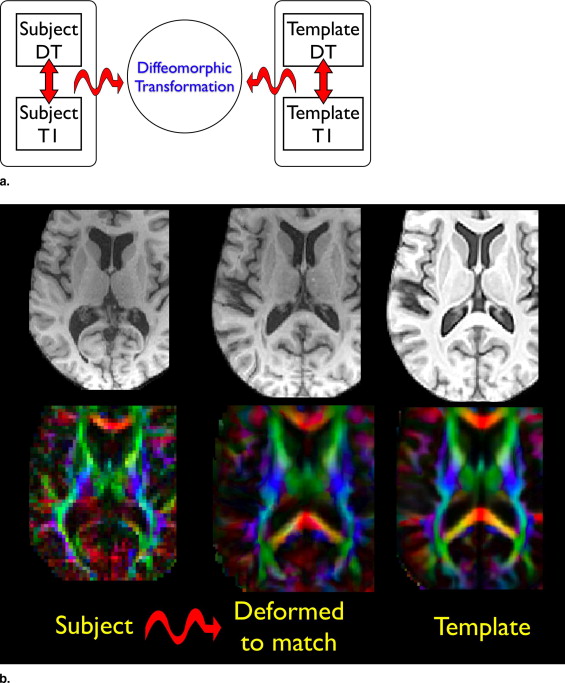
Symmetric diffeomorphic registration

Get Radiology Tree app to read full this article<

Dshape((x,0),(x,1))=minυ∫10∥υ(x,t)∥dt. D

(

)

(

)

min

⁡

∫

‖

(

)

‖

Get Radiology Tree app to read full this article<

D2shape((x,0),(x,1))+Dsimilarity((x,1),I,J). D

(

)

(

)

(

)

Get Radiology Tree app to read full this article<

Symmetric DT Diffeomorphic Registration

Get Radiology Tree app to read full this article<

∥D1−D2∥DV=Tr((D1−D2)2)−13(Tr(D1)−Tr(D2))2.−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√ ‖

−

‖

Tr((D

−

)

−

(Tr(D

)

−

Tr(D

))

Get Radiology Tree app to read full this article<

∥IDT(1(x))−JDT(2(x))∥2DV, ‖

(

)

−

(

)

‖

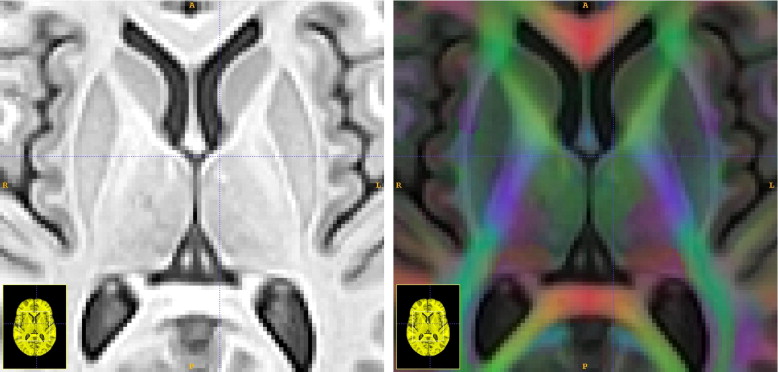
where we apply the transformations Φ 1 and Φ 2 to the DT images. Local deformations of the DT image should preserve orientation of white matter fibers in relation to the anatomy. Thus, to warp and reorient the DT images, we use the preservation of principle directions method, as given by Alexander and Gee ( ). Preservation of principle directions guarantees that tensors properly reorient under a warping.

Get Radiology Tree app to read full this article<

SyNMN with T1 and DT

Get Radiology Tree app to read full this article<

D2shape((x,0),(x,1))+DMVsim((x,1),I2,J2). D

(

)

(

)

(

)

Get Radiology Tree app to read full this article<

DMVsim(I2,J2,)=ω1(x)MI(IT1(1),JT1(2))+ω2(x)∥IDT(1)−JDT(2))∥2DV D

(

)

(

)

(

)

(

)

(

)

‖

(

)

−

(

)

‖

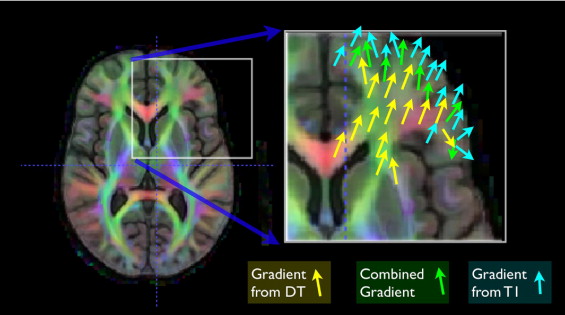
where MI is the mutual information (defined in the usual way) and the ω__i weights each similarity term as a function of the domain. If this term is optimized, we write I 2 ( ϕ__1 (0.5)) ≈ J 2 ( ϕ__2 (0.5)). Our previous work in curve matching ( ) showed that weights that vary across the spatial domain allow results that may be superior to results found with constant weighting terms. These combined gradient functions, used at each iteration, are illustrated in Figure 5 . The sum of the weighting functions is always constrained to add to one. We also normalize each similarity derivative such that its maximum displacement, before weighting, is on the order of a single voxel. This latter step aids in making a fair combination of the different gradients.

Get Radiology Tree app to read full this article<

Cohort and Image Dataset

Get Radiology Tree app to read full this article<

Cohort

Get Radiology Tree app to read full this article<

Imaging Parameters

Get Radiology Tree app to read full this article<

Results

Get Radiology Tree app to read full this article<

Performance Evaluation

Get Radiology Tree app to read full this article<

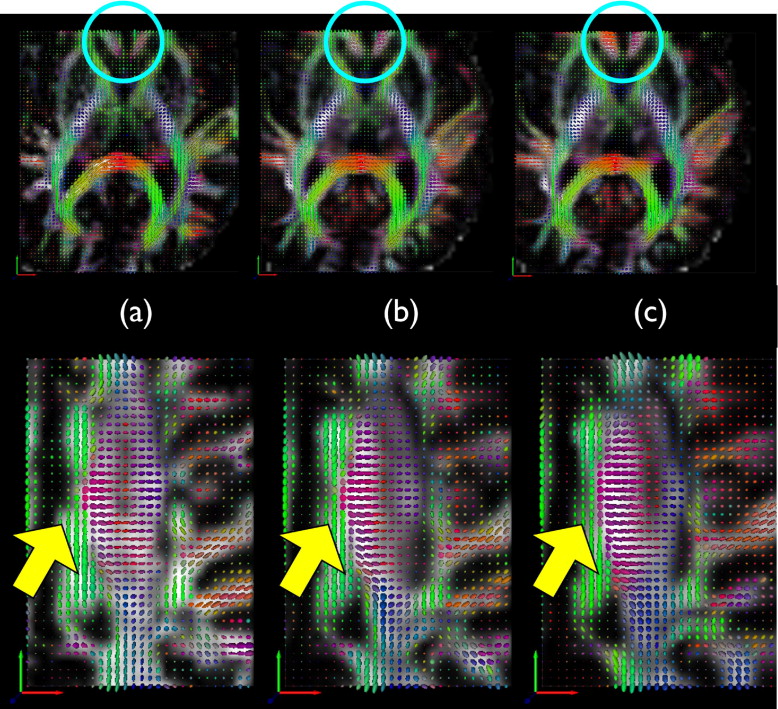
Qualitative Assessment

Get Radiology Tree app to read full this article<

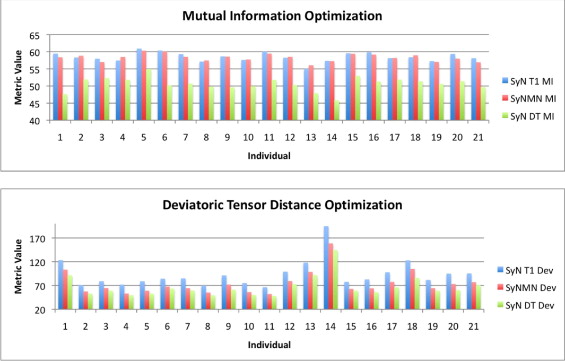
Quantitative Assessment of Optimization Performance

Get Radiology Tree app to read full this article<

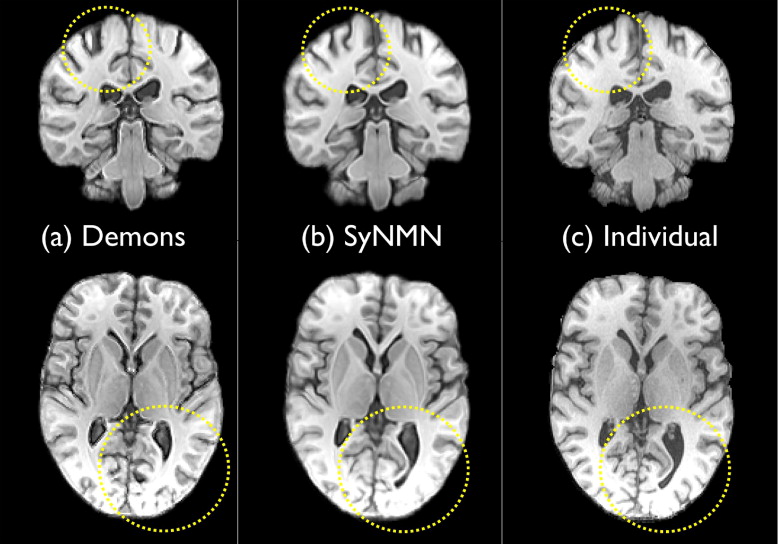
Evaluation of Hippocampus Segmentation Quality

Get Radiology Tree app to read full this article<

Table 1

Dice Overlap between Labeled Hippocampi Generated by Expert Manual Segmentation and Automatic Segmentation by SyN with T1, SyNMN with DT and T1 data, and the Demons Method

Evaluation of Automated Hippocampus Segmentation Subject SyN Dice Left SyN Dice Right SyNMN Dice Left SyNMN Dice Right Demons Dice Left Demons Dice Right 1 0.776 0.837 0.821 0.818 0.732 0.802 2 0.790 0.889 0.805 0.878 0.778 0.862 3 0.854 0.833 0.888 0.836 0.837 0.841 4 0.819 0.834 0.879 0.851 0.831 0.834 5 0.793 0.878 0.835 0.903 0.773 0.828 6 0.853 0.887 0.876 0.866 0.822 0.853 7 0.826 0.834 0.857 0.813 0.779 0.813 8 0.857 0.861 0.871 0.874 0.847 0.830 9 0.922 0.910 0.905 0.924 0.823 0.824 tbi 10 0.862 0.858 0.838 0.857 0.800 0.846 tbi 11 0.873 0.893 0.887 0.863 0.854 0.881 tbi 12 0.840 0.872 0.868 0.856 0.799 0.846 tbi 13 0.789 0.838 0.781 0.873 0.682 0.723 tbi 14 0.786 0.814 0.786 0.799 0.694 0.792 tbi 15 0.882 0.886 0.862 0.885 0.801 0.762 tbi 16 0.868 0.887 0.871 0.862 0.861 0.859 tbi 17 0.898 0.880 0.905 0.886 0.791 0.877 tbi 18 0.860 0.895 0.891 0.906 0.790 0.858 tbi 19 0.860 0.849 0.871 0.869 0.790 0.856 tbi 20 0.883 0.882 0.899 0.838 0.790 0.807 tbi 21 0.786 0.878 0.812 0.880 0.789 0.681 Average 0.845 0.866 0.860 0.864 0.794 0.823t -Test vs. demons 6.49 6.91 0P value vs. demons 8.57E-08 2.20E-08 1

DT, diffusion tensor; SyN, symmetric normalization; SyNMN, symmetric normalization for multivariate neuroanatomy.

Aggregate performance difference, for both left and right hippocampi, is assessed by pairwise t -test. SyN and SyNMN show similar performance.

Get Radiology Tree app to read full this article<

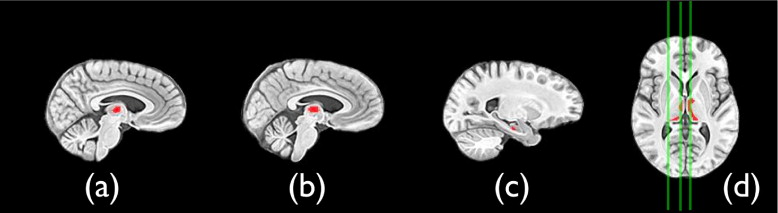
Multivariate Effects of TBI

Get Radiology Tree app to read full this article<

Discussion

Get Radiology Tree app to read full this article<

References

1. Furlow B.: Diagnostic imaging of traumatic brain injury. Radiol Technol 2006; 78: pp. 145-156. quiz 157–159.
2. Hoge C.W., McGurk D., Thomas J.L., et. al.: Mild traumatic brain injury in U.S. Soldiers returning from Iraq. N Engl J Med 2008; 358: pp. 453-463.
3. Kraus M.F., Susmaras T., Caughlin B.P., et. al.: White matter integrity and cognition in chronic traumatic brain injury: a diffusion tensor imaging study. Brain 2007; 130: pp. 2508-2519.
4. Mendez C.V., Hurley R.A., Lassonde M., et. al.: Mild traumatic brain injury: neuroimaging of sports-related concussion. J Neuropsychiatry Clin Neurosci 2005; 17: pp. 297-303.
5. Chen J.K., Johnston K.M., Petrides M., et. al.: Neural substrates of symptoms of depression following concussion in male athletes with persisting postconcussion symptoms. Arch Gen Psychiatry 2008; 65: pp. 81-89.
6. Kim J., Avants B., Patel S., et. al.: Structural consequences of diffuse traumatic brain injury: a large deformation tensor-based morphometry study. Neuroimage 2008; 39: pp. 1014-1026.
7. Levin H.S.: Neuroplasticity following non-penetrating traumatic brain injury. Brain Inj 2003; 17: pp. 665-674.
8. Miles L., Grossman R.J., Johnson G., et. al.: Short-term DTI predictors of cognitive dysfunction in mild traumatic brain injury. Brain Inj 2008; 22: pp. 115-122.
9. Sidaros A., Engberg A.W., Sidaros K., et. al.: Diffusion tensor imaging during recovery from severe traumatic brain injury and relation to clinical outcome: a longitudinal study. Brain 2008; 131: pp. 559-572.
10. Gale S.D., Baxter L., Roundy N., et. al.: Traumatic brain injury and grey matter concentration: a preliminary voxel based morphometry study. J Neurol Neurosurg Psychiatry 2005; 76: pp. 984-988.
11. Tomaiuolo F., Carlesimo G.A., Di Paola M., et. al.: Gross morphology and morphometric sequelae in the hippocampus, fornix, and corpus callosum of patients with severe non-missile traumatic brain injury without macroscopically detectable lesions: a T1 weighted MRI study. J Neurol Neurosurg Psychiatry 2004; 75: pp. 1314-1322.
12. Salmond C.H., Chatfield D.A., Menon D.K., et. al.: Cognitive sequelae of head injury: involvement of basal forebrain and associated structures. Brain 2005; 128: pp. 189-200.
13. Graham D.I., Maxwell W.L., Adams J.H., et. al.: Novel aspects of the neuropathology of the vegetative state after blunt head injury. Prog Brain Res 2005; 150: pp. 445-455.
14. Zhang L., Yang K.H., King A.I.: A proposed injury threshold for mild traumatic brain injury. J Biomech Eng 2004; 126: pp. 226-236.
15. Maxwell W.L., Pennington K., MacKinnon M.A., et. al.: Differential responses in three thalamic nuclei in moderately disabled, severely disabled and vegetative patients after blunt head injury. Brain 2004; 127: pp. 2470-2478.
16. Adams J.H., Graham D.I., Jennett B.: The neuropathology of the vegetative state after an acute brain insult. Brain 2000; 123: pp. 1327-1338.
17. Maxwell W.L., MacKinnon M.A., Smith D.H., et. al.: Thalamic nuclei after human blunt head injury. J Neuropathol Exp Neurol 2006; 65: pp. 478-488.
18. Kotapka M.J., Graham D.I., Adams J.H., et. al.: Hippocampal pathology in fatal human head injury without high intracranial pressure. J Neurotrauma 1994; 11: pp. 317-324.
19. Ahn H.Y., Kim S.H., Han B.S., et. al.: Focal lesions of the corticospinal tract demonstrated by diffusion tensor imaging in patients with diffuse axonal injury. NeuroRehabilitation 2006; 21: pp. 239-243.
20. Bazarian J.J., Zhong J., Blyth B., et. al.: Diffusion tensor imaging detects clinically important axonal damage after mild traumatic brain injury: a pilot study. J Neurotrauma 2007; 24: pp. 1447-1459.
21. Mac Donald C.L., Dikranian K., Bayly P., et. al.: Diffusion tensor imaging reliably detects experimental traumatic axonal injury and indicates approximate time of injury. J Neurosci 2007; 27: pp. 11869-11876.
22. Lee H.W., Choi C.G., Chun M.H.: Usefulness of diffusion tensor imaging for evaluation of motor function in patients with traumatic brain injury: three case studies. J Head Trauma Rehabil 2006; 21: pp. 272-278.
23. Song S.K., Sun S.W., Ramsbottom M.J., et. al.: Dysmyelination revealed through MRI as increased radial (but unchanged axial) diffusion of water. Neuroimage 2002; 17: pp. 1429-1436.
24. Mori S., Zhang J.: Principles of diffusion tensor imaging and its applications to basic neuroscience research. Neuron 2006; 51: pp. 527-539.
25. Ardekani A.B., Bappal A., D’Angelo D., et. al.: Brain morphometry using diffusion-weighted magnetic resonance imaging: application to schizophrenia. Neuroreport 2005; 16: pp. 1455-1459.
26. Sugiyama S., Kondo T., Higano S., et. al.: Diffusion tensor imaging fiber tractography for evaluating diffuse axonal injury. Brain Inj 2007; 21: pp. 413-419.
27. Levin H.S., Benavidez D.A., Verger-Maestre K., et. al.: Reduction of corpus callosum growth after severe traumatic brain injury in children. Neurology 2000; 54: pp. 647-653.
28. Ewing-Cobbs L.E., Hasan K.M., Prasad M.R., et. al.: Corpus callosum diffusion anisotropy correlates with neuropsychological outcomes in twins disconcordant for traumatic brain injury. AJNR Am J Neuroradiol 2006; 27: pp. 879-881.
29. Hashimoto K., Okumura A., Shinoda J., et. al.: Tensor magnetic resonance imaging in a case of mild traumatic brain injury with lowered verbal intelligence quotient. J Rehabil Med 2007; 39: pp. 418-420.
30. Inglese M., Makani S., Johnson G., et. al.: Diffuse axonal injury in mild traumatic brain injury: a diffusion tensor imaging study. J Neurosurg 2005; 103: pp. 298-303.
31. Nakayama N., Okumura A., Shinoda J., et. al.: Evidence for white matter disruption in traumatic brain injury without macroscopic lesions. J Neurol Neurosurg Psychiatry 2006; 77: pp. 850-855.
32. Xu J., Rasmussen I.A., Lagopoulos J., et. al.: Diffuse axonal injury in severe traumatic brain injury visualized using high-resolution diffusion tensor imaging. J Neurotrauma 2007; 24: pp. 753-765.
33. Le T.H., Mukherjee P., Henry R.G., et. al.: Diffusion tensor imaging with three-dimensional fiber tractography of traumatic axonal shearing injury: an imaging correlate for the posterior callosal “disconnection” syndrome: case report. Neurosurgery 2005; 56: pp. 189.
34. Yasokawa Y.T., Shinoda J., Okumura A., et. al.: Correlation between diffusion-tensor magnetic resonance imaging and motor-evoked potential in chronic severe diffuse axonal injury. J Neurotrauma 2007; 24: pp. 163-173.
35. Han B.S., Kim S.H., Kim O.L., et. al.: Recovery of corticospinal tract with diffuse axonal injury: a diffusion tensor image study. NeuroRehabilitation 2007; 22: pp. 151-155.
36. Kantarci K., Jack C.R., Xu Y.C., et. al.: Mild cognitive impairment and Alzheimer disease: regional diffusivity of water. Radiology 2001; 219: pp. 101-107.
37. Chappell M.H., Ulug A.M., Zhang L., et. al.: Distribution of microstructural damage in the brains of professional boxers: a diffusion MRI study. J Magn Reson Imaging 2006;
38. Ray K.M., Wang H., Chu Y., et. al.: Mild cognitive impairment: apparent diffusion coefficient in regional gray matter and white matter structures. Radiology 2006; 241: pp. 197-205.
39. Salmond C.H., Menon D.K., Chatfield D.A., et. al.: Diffusion tensor imaging in chronic head injury survivors: correlations with learning and memory indices. Neuroimage 2006; 29: pp. 117-124.
40. Duan Y., Li X., Xi Y.: Thalamus segmentation from diffusion tensor magnetic resonance imaging. Int J Biomed Imaging 2007; 2007: pp. 90216.
41. Wiegell M.R., Tuch D.S., Larsson H.B.W., et. al.: Automatic segmentation of thalamic nuclei from diffusion tensor magnetic resonance imaging. Neuroimage 2003; 19: pp. 391-401.
42. Miller M.I., Christensen G.E., Amit Y., et. al.: Mathematical textbook of deformable neuroanatomies. Proc Natl Acad Sci U S A 1993; 90: pp. 11944-11948.
43. Park H.-J., Kubicki M., Shenton M.E., et. al.: Spatial normalization of diffusion tensor MRI using multiple channels. Neuroimage 2003; 20: pp. 1995-2009.
44. Studholme C.: Dense feature deformation morphometry: incorporating DTI data into conventional MRI morphometry. Med Image Anal 2008; Apr 16. Epub ahead of print.
45. Miller M.I., Beg M.F., Ceritoglu C., et. al.: Increasing the power of functional maps of the medial temporal lobe by using large deformation diffeomorphic metric mapping. PNAS 2005; 102: pp. 9685-9690.
46. Yan C., Miller M.I., Winslow R.L., et. al.: Large deformation diffeomorphic metric mapping of vector fields. TMI 2005; 24: pp. 1216-1230.
47. Zhang H., Yushkevich P.A., Alexander D.C., et. al.: Deformable registration of diffusion tensor MR images with explicit orientation optimization. Med Image Anal 2006; 10: pp. 764-785.
48. Zhang H., Avants B.B., Yushkevich P.A., et. al.: High-dimensional spatial normalization of diffusion tensor images improves the detection of white matter differences: an example study using amyotrophic lateral sclerosis. IEEE Trans Med Imaging 2007; 26: pp. 1585-1597.
49. Mangin J., Poupon C., Clark C., et. al.: Distortion correction and robust tensor estimation for MR diffusion imaging. Med Image Anal 2003; 6: pp. 191-198.
50. Miller M., Trouve A., Younes L.: On the metrics and Euler-Lagrange equations of computational anatomy. Annu Rev Biomed Eng 2002; 4: pp. 375-405.
51. Avants B.B., Epstein C.L., Grossman M., et. al.: Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Med Image Anal 2008; 12: pp. 26-41.
52. Alexander D.C., Pierpaoli C., Basser P.J., et. al.: Spatial transformations of diffusion tensor magnetic resonance images. IEEE Trans Med Imaging 2001; 20: pp. 1131-1139.
53. Arsigny V., Fillard P., Pennec X., et. al.: Log-Euclidean metrics for fast and simple calculus on diffusion tensors. Magn Reson Med 2006; 56: pp. 411-421.
54. Kindlmann G., Estepar R.S., Niethammer M., et. al.: Geodesic-loxodromes for diffusion tensor interpolation and difference measurement. Conference on Medical Image Computing and Computer Aided Intervention 2007; 10: pp. 1-9.
55. Avants B.B., Gee J.C.: Formulation and evaluation of variational curve matching with prior constraints.Gee J.C.Maintz J.B.A.Vannier M.W.Biomedical image registration.2003.Springer-VerlagHeidelberg, Germany:pp. 21-30.
56. Hermosillo G., Chefd’Hotel C., Faugeras O.: A variational approach to multi-modal image matching. Intl J Comp Vis 2002; 50: pp. 329-343.
57. Avants B.B., Giannetta J., Gee J.C., et. al.: Analyzing long term effects of cocaine exposure on adolescent brain structure with symmetric diffeomorphisms.2006. New York City.
58. Beg M.F., Khan A.: Symmetric data attachment terms for large deformation image registration. IEEE Trans Med Imaging 2007; 26: pp. 1179-1189.
59. Thirion J.P.: Non-rigid matching using demons. IEEE Computer Vision and Pattern Recognition 1996; pp. 245-251.
60. Yushkevich P.A., Detre J.A., Mechanic-Hamilton A., et. al.: Hippocampus-specific fMRI group activation analysis using the continuous medial representation. Neuroimage 2007; 35: pp. 1516-1530.
61. Langers D.R.M., Jansen J.F.A., Backes W.H.: Enhanced signal detection in neuroimaging by means of regional control of the global false discovery rate. Neuroimage 2007; 38: pp. 43-56.
62. Hammers A., Heckemann R., Koepp M.J., et. al.: Automatic detection and quantification of hippocampal atrophy on MRI in temporal lobe epilepsy: a proof-of-principle study. Neuroimage 2007; 36: pp. 38-47.
63. O’Sullivan M., Singhal S., Charlton R., et. al.: Diffusion tensor imaging of thalamus correlates with cognition in CADASIL without dementia. Neurology 2004; 62: pp. 702-707.
64. Schiff N.D., Giacino J.T., Kalmar K., et. al.: Behavioural improvements with thalamic stimulation after severe traumatic brain injury. Nature 2007; 448: pp. 600-603.
65. Drevets W.C.: Neuroimaging studies of mood disorders. Biol Psychiatry 2000; 48: pp. 813-829.
66. McAllister T.W.: Traumatic brain injury and psychosis: what is the connection?. Semin Clin Neuropsychiatry 1998; 3: pp. 211-223.
67. Sydykova D., Stahl R., Dietrich O., et. al.: Fiber connections between the cerebral cortex and the corpus callosum in Alzheimer’s disease: a diffusion tensor imaging and voxel-based morphometry study. Cereb Cortex 2007; 17: pp. 2276-2282.
68. Naganawa S., Sato C., Ishihra S., et. al.: Serial evaluation of diffusion tensor brain fiber tracking in a patient with severe diffuse axonal injury. AJNR Am J Neuroradiol 2004; 25: pp. 1553-1556.
69. Rutgers D.R., Toulgoat F., Cazejust J., et. al.: White matter abnormalities in mild traumatic brain injury: a diffusion tensor imaging study. AJNR Am J Neuroradiol 2008; 29: pp. 514-519.
70. Wilde E.A., Bigler E.D., Haider J.M., et. al.: Vulnerability of the anterior commissure in moderate to severe pediatric traumatic brain injury. J Child Neurol 2006; 21: pp. 769-776.

Multivariate Analysis of Structural and Diffusion Imaging in Traumatic Brain Injury

Rationale and Objectives

Materials and Methods

Results

Conclusions

Materials and methods

Theory for Multivariate Image Processing

Multivariate datasets

Symmetric diffeomorphic registration

Symmetric DT Diffeomorphic Registration

SyNMN with T1 and DT

Cohort and Image Dataset

Cohort

Imaging Parameters

Results

Performance Evaluation

Qualitative Assessment

Quantitative Assessment of Optimization Performance

Evaluation of Hippocampus Segmentation Quality

Multivariate Effects of TBI

Discussion

References

Further Reading

Abstracts of Funded National Institutes of Health Grants

Advances in Radiological Image Analysis from MICCAI 2007

Automated 11 C-PiB Standardized Uptake Value Ratio