Pulmonary Kinematics From Image Data

The effects of certain lung pathologies include alterations in lung physiology negatively affecting pulmonary compliance. Current approaches to diagnosis and treatment assessment of lung disease commonly rely on pulmonary function testing. Such testing is limited to global measures of lung function, neglecting regional measurements, which are critical for early diagnosis and localization of disease. Increased accessibility to medical image acquisition strategies with high spatiotemporal resolution coupled with the development of sophisticated intensity-based and geometric registration techniques has resulted in the recent exploration of modeling pulmonary motion for calculating local measures of deformation. In this review, the authors provide a broad overview of such research efforts for the estimation of pulmonary deformation. This includes discussion of various techniques, current trends in validation approaches, and the public availability of software and data resources.

“Ceiinosssttuu,” or so wrote the great 17th-century scientist Robert Hooke in describing the response of a spring to an applied force in Latin anagrammatic form. 1

1 Rearranged, the letters form the Latin phrase “ut tensio sic vis,” which, roughly translated, reads “As extension, so is the force” .

Today it is easily recognized in its more ubiquitous form

F=−kΔx, F

−

where Δ x is the change in the length of a spring in response to the applied force, F , and k , which characterizes a mechanical property of the spring, is known as the spring constant. The formulation of Hooke’s law marks a seminal moment in the study of material properties and their responses to applied forces. Analogously, a similar relationship characterizing elastic properties of the lung is approximated from the pressure-volume-compliance relationship :

ΔP=1CΔV, Δ

where C is the volumetric compliance characterizing the properties of the lung (the inverse is called the elastance), and Δ P is the change in pressure, which results in the change of volume, Δ V .

The importance of characterizing biomechanical properties includes the study of pulmonary physiology. Lung disease is one of the leading causes of death in the United States, not only affecting an individual’s respiratory function but having extensive vascular sequelae. Pulmonary function testing, the gold standard for diagnosing lung disease, provides global information about lung function and depends on race, age, gender, and body habitus to interpret the normalcy of a patient’s respiratory parameters. Numerous attempts have been made to study the regional mechanics of the lung ex vivo. However, the power of medical imaging can be harnessed to noninvasively study pulmonary morphology and function. When coupled with image processing techniques such as nonrigid registration, these image data provide both global and regional quantitative assessments of the lung. This approach can be used not only to quantify motion in healthy individuals but to investigate the presence and evolution of disease in patients and populations.

Normal pulmonary anatomy and physiology

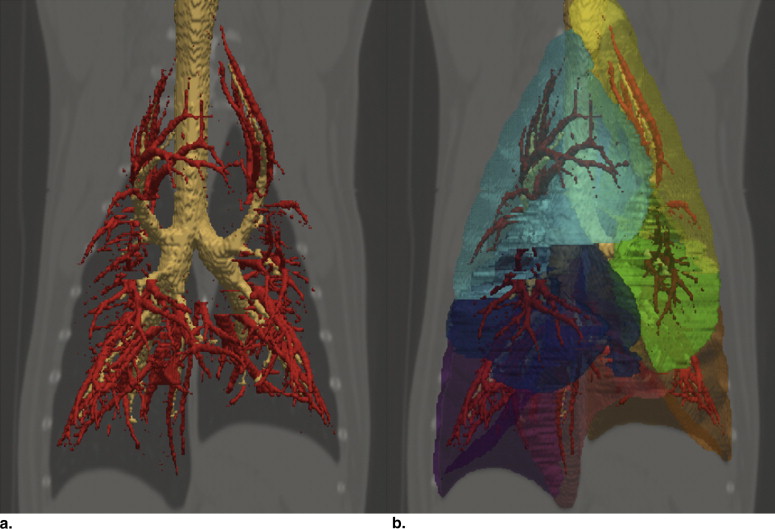
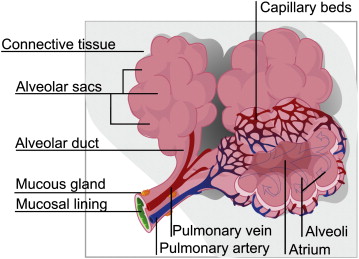
The lungs play many critical roles in physiology, such as gas exchange, rapid modulation of blood pH, thermoregulation, and immunoprotection. Structurally, the lung can be described as an elastic body, an elaborate network of fibers connecting the vasculature, airways, and pulmonary interstitium ( Fig 1 ). Normal lung tissue has a homogeneous appearance delineated by lobular boundaries and airway and vascular trees.

Get Radiology Tree app to read full this article<

Pulmonary Pathophysiology

Get Radiology Tree app to read full this article<

Pulmonary Function Testing

Get Radiology Tree app to read full this article<

Early Studies of Pulmonary Biomechanics

Get Radiology Tree app to read full this article<

Pulmonary Imaging

Get Radiology Tree app to read full this article<

Pulmonary kinematics

Get Radiology Tree app to read full this article<

Deformation Analysis

Get Radiology Tree app to read full this article<

Fair=CTwater−CTCTwater−CTair, F

air

water

−

water

−

air

where CT air is the intensity of a region of known 100% air content, such as the center of the trachea, and CT water is the intensity of a region of known 100% water content, such as the heart ventricles .

Get Radiology Tree app to read full this article<

Fair=−HU1000. F

air

−

1000

Get Radiology Tree app to read full this article<

ΔVVexp=Fins−FexpFexp⋅(1−Fins)=1000HUins−HUexpHUexp⋅(1000+HUins). Δ

exp

ins

−

exp

(

−

ins

)

1000

ins

−

exp

(

1000

ins

)

Get Radiology Tree app to read full this article<

x=μ+X,y=v+Y,z=ξ+Z. x

Get Radiology Tree app to read full this article<

F=∇xx=⎡⎣⎢⎢⎢∂x∂X∂y∂X∂z∂X∂x∂Y∂y∂Y∂z∂Y∂x∂Z∂y∂Z∂z∂Z⎤⎦⎥⎥⎥, F

∇

[

∂

]

or, in terms of the components of the transformation field,

F=⎡⎣⎢⎢⎢∂μ∂X∂ν∂X∂ξ∂X∂μ∂Y∂ν∂Y∂ξ∂Y∂μ∂Z∂ν∂Z∂ξ∂Z⎤⎦⎥⎥⎥=I, F

[

∂

]

where I is the identity matrix. Depending on the form of τ, the partial derivatives in equation 8 are either approximated using finite differences or, if τ is continuous, analytically derived.

Get Radiology Tree app to read full this article<

∣∣F∣∣=dVxdVx, |

where dV represents an infinitesimal volume element, and | · | denotes the determinant operation (compare to equation 5 ). | F | is often referred to as the Jacobian and is useful for tabulating compliance measures (see equation 2 ). The principal focus of this review is providing an overview of the various methods that have been proposed to obtain the transformation, τ, from image data of the lungs from which these useful biomechanical measures can be calculated.

Get Radiology Tree app to read full this article<

Intensity-based Estimation of τ From Image Data

Get Radiology Tree app to read full this article<

Table 1

Sampling of Recent Intensity-based Approaches to Inferring Lung Motion

Source Similarity Regularization Modality Castillo COF HS CT Guerrero et al OF HS CT Dawood OF HS/LK PET Christensen SSD_L_ , IC CT Boldea SSD/APLDM Gaussian CT Dougherty SSD/LI LK CT Li et al ∗ SSD_L_ , IC CT Reinhardt et al SSD LE, IC CT Cook SSD SyN CT Cook MI SyN CT Cook CC SyN CT Gee CC LE MRI Sarrut SSD FFD CT Sarrut OF/APLDM Gaussian CT Voorhees CC LK t-MRI Wang Demons Gaussian CT Wu SSD FFD CT Wu Demons Gaussian CT

APLDM, a priori lung density modification; CC, cross-correlation; COF, compressible optical flow; CT, computed tomography; FFD, freeform deformation; HS, Horn-Schunck; IC, inverse consistency; L, linear operator; LE, linear elastic; LI, Laplacian-filtered images; LK, Lucas-Kanade; MRI, magnetic resonance imaging; OF, optical flow; SSD, sum of squares difference; SyN, symmetric normalization; t-MRI, tagged magnetic resonance imaging.

Get Radiology Tree app to read full this article<

Table 2

Sampling of Recent Geometric Approaches to Inferring Lung Motion

Source Similarity Regularization Feature Type Modality Gorbunova Currents Gaussian Vasculature, lung surfaces CT Hilsmann et al ED TPS Vessel bifurcations CT Plathow ED EBS Lung surface CT Li ∗ ED TPS Airway bifurcations CT Tustison JHCT DMFFD Vasculature, lung surfaces CT Cai ED LI Tagging grid cell centroids t-HHe MRI Tustison JHCT DMFFD Tagging planes t-HHe MRI

CT, computed tomography; DMFFD, directly manipulated freeform deformation; EBS, elastic-body splines; ED, Euclidean distance between corresponding features; JHCT, Jensen-Havrda-Charvat-Tsallis divergence; LI, linear interpolation; t-HHe MRI, tagged hyperpolarized 3 He magnetic resonance imaging; TPS, thin-plate splines.

Get Radiology Tree app to read full this article<

Optical Flow

Get Radiology Tree app to read full this article<

I(x,t)=I(x+δx,t+δt), I

(

)

(

)

where x denotes spatial location, and t denotes acquisition time. Expanding the right side of equation 10 using Taylor’s series expansion yields the following relationship:

I(x,t)=I(x,t)+∇I⋅δx+It⋅δt+O2. I

(

)

(

)

∇

Get Radiology Tree app to read full this article<

∇I⋅v+It=0, ∇

where v=δxδt v

t is the sought-after displacement. Because of the ill-posed nature of the problem (ie, there is only one equation for determining the multiple components of v ), explicit regularization of the velocity field is used. In the original contribution of Horn and Schunck , this involves penalization of deviations from an n -dimensional smooth field measured by

ϵsmooth=∥∇v∥2=∑ni=1∑nj=1(∂vi∂xj)2. ϵ

smooth

‖

∇

‖

∑

(

∂

)

Get Radiology Tree app to read full this article<

vn+1=vn−∇I(vn⋅∇I+Itλ2+∣∣∇I∣∣2), v

−

∇

(

∇

)

where λ is a user-specified weighting term that modulates the solution between contributions of ϵ smooth and ϵ optical flow . This technique has been used in recently reported research .

Get Radiology Tree app to read full this article<

v=It∇I∣∣∇I∣∣2+I2t. v

∇

Get Radiology Tree app to read full this article<

Compressible Optical Flow

Get Radiology Tree app to read full this article<

SSD(I,J)=∫Ω[I(x)−J(x)]2dΩ, SSD

(

)

∫

[

(

)

−

(

)

]

where Ω denotes the region over which the metric is calculated. However, for a CT acquisition of deformable tissue, such as the lung, this assumption is invalid because of density changes during deformation. If we let I ( x , t ) denote the density function within an object (which is, by definition, linearly proportional to the CT intensity) and assume conservation of mass of that object over the course of deformation, the standard continuity equation from continuum mechanics can be derived in differential form (see, eg, Chadwick ):

∇I⋅v+I∇⋅v+It=0. ∇

∇

Get Radiology Tree app to read full this article<

A Priori Lung Density Modification

Get Radiology Tree app to read full this article<

I′1(x)=I1(x)+ρ2(z′)−ρ1(z), I

′

(

)

(

)

(

′

)

−

(

)

where I′1(x) I

′

(

) is the modified pixel value at x on slice z , ρ 1 ( z ) is mean density at slice z of I 1 , and ρ 2 ( z ′) is the mean density of image I 2 at the linearly interpolated slice location z ′. The effectiveness of the APLDM preprocessing step was demonstrated by Sarrut et al and showed improvement in registering the thorax between inspiratory and expiratory scans using a modified SSD metric. Two different explicit regularization models, Gaussian and linear elastic, were compared, with the Gaussian transformation showing the biggest improvement in matching expert-segmented landmarks after registration using APLDM (from 13.1-mm average initial distance to 2.7 mm for the Gaussian model and 3.0 mm for linear elastic regularization).

Get Radiology Tree app to read full this article<

Other Similarity Metrics

Get Radiology Tree app to read full this article<

CC(I,J)=⟨I¯∥∥I¯∥∥,J¯¯∥∥J¯¯∥∥⟩, CC

(

)

〈

‖

〉

where ⟨⋅,⋅⟩ 〈

〉 and ∥⋅∥ ‖

‖ denote the inner product and Euclidean norm, respectively, calculated within the voxel neighborhood.

Get Radiology Tree app to read full this article<

Regularization Models and Symmetric Transformation Considerations

Get Radiology Tree app to read full this article<

Modeling Four-Dimensional Lung Trajectories

Get Radiology Tree app to read full this article<

Geometric Estimation of τ From Image Data

Get Radiology Tree app to read full this article<

Landmark Matching

Get Radiology Tree app to read full this article<

Matching of Curve and Surface Geometric Primitives

Get Radiology Tree app to read full this article<

MRI Tagging

Get Radiology Tree app to read full this article<

Validation

Get Radiology Tree app to read full this article<

Intensity-based Similarity Measures

Get Radiology Tree app to read full this article<

Overlap Assessment of Anatomic Contours

Get Radiology Tree app to read full this article<

Jaccard(S,T)=|S∩T||S∪T|, Jaccard

(

)

∩

∪

whereas the Dice coefficient is calculated from

Dice(S,T)=2|S∩T||S|+|T|. Dice

(

)

∩

Get Radiology Tree app to read full this article<

Expert-defined Landmarks

Get Radiology Tree app to read full this article<

TRE(τ)=1n∑ni=1[τ(pi)−qi]2−−−−−−−−−−√. TRE

(

)

∑

[

(

)

−

]

Get Radiology Tree app to read full this article<

STE(T1,T2)=1t2−t1∫t2t1dist{T1[s(t)],T2[s(t)]}dt, STE

(

)

−

∫

dist

{

[

(

)

]

[

(

)

]

}

where s ( t ) defines the curve length along the trajectory between the initial time t 1 and t . For multiple-phase data, this allows one to weight the error in the intermediate phases less than the error at the extreme phases.

Get Radiology Tree app to read full this article<

Miscellaneous Approaches

Get Radiology Tree app to read full this article<

Public resources

Get Radiology Tree app to read full this article<

Table 3

Available Software and Data Resources

Web Site Description Software http://www.itk.org Collection of image analysis algorithms, including image registration sponsored by the NIH (158) http://picsl.upenn.edu/ANTS/ Suite of image registration, segmentation, and other analysis tools (159) http://biocomp.cnb.csic.es/∼iarganda/bUnwarpJ/ Bidirectional spline-based image registration (160); available as an ImageJ plug-in http://elastix.isi.uu.nl Suite of general registration tools, including multiple similarity metrics and transforms (rigid, affine, and spline-based nonrigid) (161) http://www.fmrib.ox.ac.uk/fsl/ FMRIB Software Library: contains FLIRT (linear) and FNIRT (nonrigid) registration algorithms (162,163) Data http://www.dir-lab.com CT image and corresponding landmark evaluation data for 10 subjects across multiple phases of the respiratory cycle https://imaging.nci.nih.gov/ncia/ LIDC of the NCI (164)

CT, computed tomographic; FLIRT, FMRIB’s Linear Image Registration Tool; FMRIB, Functional Magnetic Resonance Imaging of the Brain; FNIRT, FMRIB’s Non-Linear Image Registration Tool; LIDC, Lung Image Database Consortium; NCI, National Cancer Institute; NIH, National Institutes of Health.

Get Radiology Tree app to read full this article<

Discussion

Get Radiology Tree app to read full this article<

Acknowledgment

Get Radiology Tree app to read full this article<

References

1. Searle G.F.C.: Experimental elasticity.1908.Cambridge University PressCambridge, UK
2. Simon B.A.: Non-invasive imaging of regional lung function using x-ray computed tomography. J Clin Monit Comput 2000; 16: pp. 433-442.
3. Murray J.F.Nadel J.A.Textbook of respiratory medicine.2000.W.B. Saunders CompanyPhiladelphia:
4. Lai-Fook S.J.: Stress distribution in the lung.Crystal R.G.West J.B.Weibel E.R.Barnes P.The lung: scientific foundations.1997.Lippincott-RavenPhiladelphia:pp. 1177-1186.
5. Kamm R.D.: Airway wall mechanics. Annu Rev Biomed Eng 1999; 1: pp. 47-72.
6. American Lung Association. Lung disease data: 2006. Available at: http://www.lungusa.org/assets/documents/publications/lung-disease-data/LDD_2006.pdf . Accessed December 29, 2010.
7. Pratt P.C.: Emphysema and chronic airways disease.Dail D.H.Hamar S.P.Pulmonary pathology.1988.SpringerNew York:pp. 654-659.
8. Silvers G.W., Petty T.L., Stanford R.E.: Elastic recoil changes in early emphysema. Thorax 1980; 35: pp. 490-495.
9. Petty T.L., Silvers G.W., Stanford R.E.: Mild emphysema is associated with reduced elastic recoil and increased lung size but not with air-flow limitation. Am Rev Respir Dis 1987; 136: pp. 867-871.
10. Fulmer J.D., Roberts W.C., von Gal E.R., et. al.: Morphologic-physiologic correlates of the severity of fibrosis and degree of cellularity in idiopathic pulmonary fibrosis. J Clin Invest 1979; 63: pp. 665-676.
11. Gay S.E., Kazerooni E.A., Toews G.B., et. al.: Idiopathic pulmonary fibrosis: predicting response to therapy and survival. Am J Respir Crit Care Med 1998; 157: pp. 1063-1072.
12. Knight J., Murphy T.M., Browning I.: The lung in sickle cell disease. Pediatr Pulmonol 1999; 28: pp. 205-216.
13. Gold W.: Pulmonary function testing.Murray J.F.Nadel J.A.Textbook of Respiratory Medicine.2000.W. B. SaundersPhiladelphia:pp. 783-804.
14. Crapo R.O.: Pulmonary-function testing. N Engl J Med 1994; 331: pp. 25-30.
15. Mead J., Whittenberger J.: Physical properties of human lungs measured during spontaneous respiration. J Appl Phys 1953; 5: pp. 779-796.
16. Turner J.M., Mead J., Wohl M.E.: Elasticity of human lungs in relation to age. J Appl Phys 1968; 25: pp. 664-671.
17. West J.B.: Distribution of mechanical stress in the lung, a possible factor in localisation of pulmonary disease. Lancet 1971; 1: pp. 839-841.
18. Carton R.W., Dainauskas J., Tews B., et. al.: Isolation and study of the elastic tissue network of the lung in three dimensions. Am Rev Respir Dis 1960; 82: pp. 186-194.
19. D’Angelo E.: Stress-strain relationships during uniform and non uniform expansion of isolated lungs. Respir Physiol 1975; 23: pp. 87-107.
20. Lee G.C., Frankus A.: Elasticity properties of lung parenchyma derived from experimental distortion data. Biophys J 1975; 15: pp. 481-493.
21. Liu S., Margulies S.S., Wilson T.A.: Deformation of the dog lung in the chest wall. J Appl Physiol 1990; 68: pp. 1979-1987.
22. Mead J., Takishima T., Leith D.: Stress distribution in lungs: a model of pulmonary elasticity. J Appl Physiol 1970; 28: pp. 596-608.
23. Lambert R.K., Wilson T.A.: A model for the elastic properties of the lung and their effect of expiratory flow. J Appl Physiol 1973; 34: pp. 34-48.
24. Wilson T.A.: A continuum analysis of a two-dimensional mechanical model of the lung parenchyma. J Appl Physiol 1972; 33: pp. 472-478.
25. Wilde R.D., Clement J., Hellemans J.M., et. al.: Model of elasticity of the human lung. J Appl Physiol 1981; 51: pp. 254-261.
26. Bergofsky E.H.: Relative contributions of the rib cage and the diaphragm to ventilation in man. J Appl Physiol 1964; 19: pp. 698-706.
27. Lai-Fook S.J.: Perivascular interstitial fluid pressure measured by micropipettes in isolated dog lung. J Appl Physiol 1982; 52: pp. 9-15.
28. Hogg J.C., Agarawal J.B., Gardiner A.J., et. al.: Distribution of airway resistance with developing pulmonary edema in dogs. J Appl Physiol 1972; 32: pp. 20-24.
29. Vawter D.L., Matthews F.L., West J.B.: Effect of shape and size of lung and chest wall on stresses in the lung. J Appl Physiol 1975; 39: pp. 9-17.
30. Lai-Fook S.J., Wilson T.A., Hyatt R.E., et. al.: Elastic constants of inflated lobes of dog lungs. J Appl Physiol 1976; 40: pp. 508-513.
31. Hoppin F.G., Lee G.C., Dawson S.V.: Properties of lung parenchyma in distortion. J Appl Physiol 1975; 39: pp. 742-751.
32. West J.B., Matthews F.L.: Stresses, strains, and surface pressures in the lung caused by its weight. J Appl Physiol 1972; 32: pp. 332-345.
33. van Ginneken B., ter Haar Romeny B.M., Viergever M.A.: Computer-aided diagnosis in chest radiography: a survey. IEEE Trans Med Imaging 2001; 20: pp. 1228-1241.
34. Gohagan J.K., Marcus P.M., Fagerstrom R.M., et. al.: Final results of the lung screening study, a randomized feasibility study of spiral CT versus chest x-ray screening for lung cancer. Lung Cancer 2005; 47: pp. 9-15.
35. Uppaluri R., Hoffman E.A., Sonka M., et. al.: Computer recognition of regional lung disease patterns. Am J Respir Crit Care Med 1999; 160: pp. 648-654.
36. Mayo J.R., Aldrich J., Muller N.L., et. al.: Radiation exposure at chest CT: a statement of the Fleischner Society. Radiology 2003; 228: pp. 15-21.
37. Yamamura J., Tornquist K., Buchert R., et. al.: Simulated low-dose computed tomography in oncological patients: a feasibility study. J Comput Assist Tomogr 2010; 34: pp. 302-308.
38. Isgum I., Rutten A., Prokop M., et. al.: Automated aortic calcium scoring on low-dose chest computed tomography. Med Phys 2010; 37: pp. 714-723.
39. Khan F., Bell G., Antony J., et. al.: The use of 4DCT to reduce lung dose: a dosimetric analysis. Med Dosim 2009; 34: pp. 273-278.
40. Hatabu H., Chen Q., Stock K.W., et. al.: Fast magnetic resonance imaging of the lung. Eur J Radiol 1999; 29: pp. 114-132.
41. Altes T.A., Salerno M.: Hyperpolarized gas MR imaging of the lung. J Thorac Imaging 2004; 19: pp. 250-258.
42. van Beek E.J.R., Wild J.M., Kauczor H.-U., et. al.: Functional MRI of the lung using hyperpolarized 3-helium gas. J Magn Reson Imaging 2004; 20: pp. 540-554.
43. Cai J., Chu J.C., Recine D., et. al.: CT and PET lung image registration and fusion in radiotherapy treatment planning using the chamfer-matching method. Int J Radiat Oncol Biol Phys 1999; 43: pp. 883-891.
44. Li B., Christensen G.E., Hoffman E.A., et. al.: Pulmonary CT image registration and warping for tracking tissue deformation during the respiratory cycle through 3D consistent image registration. Med Phys 2008; 35: pp. 5575-5583.
45. Reinhardt M., Ding K., Cao K., et. al.: Registration-based estimates of local lung tissue expansion compared to xenon CT measures of specific ventilation. Med Image Anal 2008; 12: pp. 752-763.
46. Werner R., Ehrhardt J., Schmidt R., et. al.: Patient-specific finite element modeling of respiratory lung motion using 4D CT image data. Med Phys 2009; 36: pp. 1500-1511.
47. Hilsmann A, Vik T, Kaus M, et al. Deformable 4DCT lung registration with vessel bifurcations. Presented at: International Conference of Computer Assisted Radiology and Surgery 2007; Berlin, Germany.
48. Tai Y.-C., Lin K.P., Hoh C.K., et. al.: Utilization of 3-D elastic transformation in the registration of chest x-ray CT and whole body PET. IEEE Trans Nucl Sci 1997; 44: pp. 1606-1612.
49. Mattes D., Haynor D.R., Vesselle H., et. al.: PET-CT image registration in the chest using free-form deformations. IEEE Trans Med Imaging 2003; 22: pp. 120-128.
50. Li B., Christensen G.E., Hoffman E.A., et. al.: Establishing a normative atlas of the human lung: intersubject warping and registration of volumetric CT images. Acad Radiol 2003; 10: pp. 255-265.
51. Guerrero T., Sanders K., Noyola-Martinez J., et. al.: Quantification of regional ventilation from treatment planning CT. Int J Radiat Oncol Biol Phys 2005; 62: pp. 630-634.
52. Hoffman E.A., McLennan G.: Assessment of the pulmonary structure-function relationship and clinical outcomes measures: quantitative volumetric CT of the lung. Acad Radiol 1997; 4: pp. 758-776.
53. Yaremko B.P., Guerrero T.M., McAleer M.F., et. al.: Determination of respiratory motion for distal esophagus cancer using four-dimensional computed tomography. Int J Radiat Oncol Biol Phys 2008; 70: pp. 145-153.
54. Zhang G., Huang T., Guerrero T., et. al.: The use of 3D optical flow method in mapping of 3D anatomical structure and tumor contours across 4D CT data. J Appl Clin Med Phys 2008; 9: pp. 59-69.
55. Guerrero T., Sanders K., Castillo E., et. al.: Dynamic ventilation imaging from four-dimensional computed tomography. Phys Med Biol 2006; 51: pp. 777-791.
56. Guerrero T., Castillo R., Sanders K., et. al.: Novel method to calculate pulmonary compliance images in rodents from computed tomography acquired at constant pressures. Phys Med Biol 2006; 51: pp. 1101-1112.
57. Guerrero T., Castillo R., Noyola-Martinez J., et. al.: Reduction of pulmonary compliance found with high-resolution computed tomography in irradiated mice. Int J Radiat Oncol Biol Phys 2007; 67: pp. 879-887.
58. Brown L.G.: A survey of image registration techniques. ACM Comput Surv 1992; 24: pp. 325-376.
59. Ibanez L., Ng L., Gee J.C., et. al.: Registration patterns: the generic framework for image registration of the Insight Toolkit. IEEE Int Symp Biomed Imaging 2002; pp. 345-348.
60. Sarrut D., Boldea V., Miguet S., et. al.: Simulation of four-dimensional CT images from deformable registration between inhale and exhale breath-hold CT scans. Med Phys 2006; 33: pp. 605-617.
61. Horn B., Schunck B.: Determining optical flow. Artif Intell 1981; 17: pp. 185-283.
62. Lucas BD. Generalized image matching by the method of differences. Doctoral dissertation, Robotics Institute, Carnegie Mellon University, 1984.
63. Dawood M., Buther F., Jiang X., et. al.: Respiratory motion correction in 3-D PET data with advanced optical flow algorithms. IEEE Trans Med Imaging 2008; 27: pp. 1164-1175.
64. Thirion J.P.: Image matching as a diffusion process: an analogy with Maxwell’s Demons. Med Image Anal 1998; 2: pp. 243-260.
65. Chadwick P.: Continuum mechanics: concise theory and problems.2nd ed.1999.DoverMineola, NY
66. Song S.M., Leahy R.M.: Computation of 3-D velocity fields from 3-D cine CT images of a human heart. IEEE Trans Med Imaging 1991; 10: pp. 295-306.
67. Castillo E., Castillo R., Zhang Y., et. al.: Compressible image registration for thoracic computed tomography images. J Med Biol Eng 2009; 29: pp. 222-233.
68. Castillo R., Castillo E., Guerra R., et. al.: A framework for evaluation of deformable image registration spatial accuracy using large landmark point sets. Phys Med Biol 2009; 54: pp. 1849-1870.
69. Gee J., Sundaram T., Hasegawa I., et. al.: Characterization of regional pulmonary mechanics from serial magnetic resonance imaging data. Acad Radiol 2003; 10: pp. 1147-1152.
70. Cook T.S., Tustison N., Biederer J., et. al.: How do registration parameters affect quantitation of lung kinematics?. Med Image Comput Comput Assist Interv Int Conf Med Image Comput Comput Assist Interv 2007; 10: pp. 817-824.
71. Voorhees A., An J., Berger K.I., et. al.: Magnetic resonance imaging-based spirometry for regional assessment of pulmonary function. Magn Reson Med 2005; 54: pp. 1146-1154.
72. Avants B.B., Epstein C.L., Grossman M., et. al.: Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Med Image Anal 2008; 12: pp. 26-41.
73. Dougherty L., Asmuth J.C., Gefter W.B.: Alignment of CT lung volumes with an optical flow method. Acad Radiol 2003; 10: pp. 249-254.
74. Dougherty L., Torigian D.A., Affusso J.D., et. al.: Use of an optical flow method for the analysis of serial CT lung images. Acad Radiol 2006; 13: pp. 14-23.
75. Bro-Nielsen M., Gramkow C.: Fast fluid registration of medical images.1996.SpringerNew York 267–276
76. Christensen G.E., Johnson H.J.: Consistent image registration. IEEE Trans Med Imaging 2001; 20: pp. 568-582.
77. Christensen G.E., Song J.H., Lu W., et. al.: Tracking lung tissue motion and expansion/compression with inverse consistent image registration and spirometry. Med Phys 2007; 34: pp. 2155-2163.
78. Klein A., Andersson J., Ardekani B.A., et. al.: Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. Neuroimage 2009; 46: pp. 786-802.
79. Boldea V., Sharp G.C., Jiang S.B., et. al.: 4D-CT lung motion estimation with deformable registration: quantification of motion nonlinearity and hysteresis. Med Phys 2008; 35: pp. 1008-1018.
80. Castillo E., Castillo R., Martinez J., et. al.: Four-dimensional deformable image registration using trajectory modeling. Phys Med Biol 2010; 55: pp. 305-327.
81. Sluimer , Schilham A., Prokop M., et. al.: Computer analysis of computed tomography scans of the lung: a survey. IEEE Trans Med Imaging 2006; 25: pp. 385-405.
82. De Nunzio G, Tommasi E, Agrusti A, et al. Automatic lung segmentation in CT images with accurate handling of the hilar region. J Digit Imaging. In press.
83. van Rikxoort E.M., de Hoop B., Viergever M.A., et. al.: Automatic lung segmentation from thoracic computed tomography scans using a hybrid approach with error detection. Med Phys 2009; 36: pp. 2934-2947.
84. Wang , Li F., Li Q.: Automated segmentation of lungs with severe interstitial lung disease in CT. Med Phys 2009; 36: pp. 4592-4599.
85. Prasad M.N., Brown M.S., Ahmad S., et. al.: Automatic segmentation of lung parenchyma in the presence of diseases based on curvature of ribs. Acad Radiol 2008; 15: pp. 1173-1180.
86. Zhang L., Hoffman E.A., Reinhardt J.M.: Atlas-driven lung lobe segmentation in volumetric X-ray CT images. IEEE Trans Med Imaging 2006; 25: pp. 1-16.
87. Pu J., Leader J.K., Zheng B., et. al.: A computational geometry approach to automated pulmonary fissure segmentation in CT examinations. IEEE Trans Med Imaging 2009; 28: pp. 710-719.
88. van Rikxoort E.M., de Hoop B., van de Vorst S., et. al.: Automatic segmentation of pulmonary segments from volumetric chest CT scans. IEEE Trans Med Imaging 2009; 28: pp. 621-630.
89. Wei Q., Hu Y., Gelfand G., et. al.: Segmentation of lung lobes in high-resolution isotropic CT images. IEEE Trans Biomed Eng 2009; 56: pp. 1383-1393.
90. Ukil S., Reinhardt J.M.: Anatomy-guided lung lobe segmentation in x-ray CT images. IEEE Trans Med Imaging 2009; 28: pp. 202-214.
91. Zheng B., Leader J.K., McMurray J.M., et. al.: Automated detection and quantitative assessment of pulmonary airways depicted on CT images. Med Phys 2007; 34: pp. 2844-2852.
92. Nakamura M., Wada S., Miki T., et. al.: Automated segmentation and morphometric analysis of the human airway tree from multidetector CT images. J Physiol Sci 2008; 58: pp. 493-498.
93. Lo P, van Ginneken B, Reinhardt JM, et al. Extraction of Airways From CT (ExACT ’09). Presented at: Second International Workshop on Pulmonary Image Analysis; 2009.
94. Agam G., Armato S.G., Wu C.: Vessel tree reconstruction in thoracic CT scans with application to nodule detection. IEEE Trans Med Imaging 2005; 24: pp. 486-499.
95. Kaftan J.N., Kiraly A.P., Bakai A., et. al.: Fuzzy pulmonary vessel segmentation in contrast enhanced CT data. Medical Imaging 2008; Image Processing 62008; 914:69141Q
96. Song G, Ramirez A-Manzanares, Gee JC. A simultaneous segmentation and regularization framework for vessel extraction in CT images. Presented at: First International Workshop on Pulmonary Image Analysis in MICCAI; 2008.
97. Bruyninckx P., Loeckx D., Vandermeulen D., et. al.: Segmentation of lung vessel trees by global optimization. Prog Biomed Optics Imaging 2009; 10: pp. 725912.1-725912.12.
98. Aykac D., Hoffman E.A., McLennan G., et. al.: Segmentation and analysis of the human airway tree from three-dimensional X-ray CT images. IEEE Trans Med Imaging 2003; 22: pp. 940-950.
99. Bookstein F.: Principal warps: thin-plate splines and the decomposition of deformations. IEEE Trans Patt Anal Machine Intell 1989; 11: pp. 567-585.
100. Urschler M, Bauer J, Ditt H, et al. SIFT and shape context for feature-based nonlinear registration of thoracic CT images. In: Proceedings of Computer Vision Approaches to Medical Image Analysis: 2nd International ECCV Workshop, 73–84.
101. Rohr K., Stiehl H.S., Sprengel R., et. al.: Landmark-based elastic registration using approximating thin-plate splines. IEEE Trans Med Imaging 2001; 20: pp. 526-534.
102. Betke M., Hong H., Thomas D., et. al.: Landmark detection in the chest and registration of lung surfaces with an application to nodule registration. Med Image Anal 2003; 7: pp. 265-281.
103. Besl J., McKay N.D.: A method for registration of 3-D shapes. IEEE Trans Patt Anal Machine Intell 1992; 14: pp. 239-256.
104. Ko J.P., Betke M.: Chest CT: automated nodule detection and assessment of change over time—preliminary experience. Radiology 2001; 218: pp. 267-273.
105. Joshi S.C., Miller M.I.: Landmark matching via large deformation diffeomorphisms. IEEE Trans Image Process 2000; 9: pp. 1357-1370.
106. Beg M.F., Miller M.I., Trouv A.E., et. al.: Computing large deformation metric mappings via geodesic flows of diffeomorphisms. Int Comput J Vision 2005; 61: pp. 139-157.
107. Glaunes J., Qiu A., Miller M.I., et. al.: Large deformation diffeomorphic metric curve mapping. Int Comput J Vision 2008; 80: pp. 317-336.
108. Gorbunova V, Durrleman S, Lo P, et al. Curve- and surface-based registration of lung CT images via currents. In: Second International Workshop on Pulmonary Image Analysis, 15–25.
109. Tustison NJ, Awate SP, Song G, et al. A new information-theoretic measure to control the robustness-sensitivity trade-off for DMFFD point-set registration. Presented at: 21st Biennial International Conference on Information Processing in Medical Imaging.
110. Tustison N.J., Avants B.B., Gee J.C.: Directly manipulated free-form deformation image registration. IEEE Trans Image Process 2009; 18: pp. 624-635.
111. Tustison N.J., Awate S.P., Gee J.C.: Information-theoretic directly manipulated free-form deformation labeled point-set registration. Insight J 2009; January-June
112. Zerhouni E., Parish D., Rogers W., et. al.: Human heart: tagging with MR imaging—a method for noninvasive assessment of myocardial motion. Radiology 1988; 169: pp. 59-63.
113. Axel L., Dougherty L.: MR imaging of motion with spatial modulation of magnetization. Radiology 1989; 171: pp. 841-845.
114. Amini A.A.Prince J.L.Measurement of cardiac deformations from MRI: physical and mathematical models.2001.KluwerAmsterdam, The Netherlands:
115. Frangi A.F., Niessen W.J., Viergever M.A.: Three-dimensional modeling for functional analysis: a review. IEEE Trans Med Imaging 2001; 20: pp. 2-25.
116. Tustison N.J., Amini A.A.: Biventricular myocardial strains via nonrigid registration of anatomical NURBS model. [corrected] IEEE Trans Med Imaging 2006; 25: pp. 94-112.
117. Ubbink S.W.J., Bovendeerd P.H.M., Delhaas T., et. al.: Towards model-based analysis of cardiac MR tagging data: relation between left ventricular shear strain and myofiber orientation. Med Image Anal 2006; 10: pp. 632-641.
118. Chen Q., Mai V.M., Bankier A.A., et. al.: Ultrafast MR grid-tagging sequence for assessment of local mechanical properties of the lungs. Magn Reson Med 2001; 45: pp. 24-28.
119. Napadow V.J., Mai V., Bankier A., et. al.: Determination of regional pulmonary parenchymal strain during normal respiration using spin inversion tagged magnetization MRI. J Magn Reson Imaging 2001; 13: pp. 467-474.
120. Willert C.E., Gharib M.: Digital particle image velocimetry. Exp Fluids 1991; 10: pp. 181-193.
121. Owers J.R.-Bradley, Fichele S., Bennattayalah A., et. al.: MR tagging of human lungs using hyperpolarized 3 He gas. J Magn Reson Imaging 2003; 17: pp. 142-146.
122. Cai J., Miller G.W., Altes T.A., et. al.: Direct measurement of lung motion using hyperpolarized helium-3 MR tagging. Int J Radiat Oncol Biol Phys 2007; 68: pp. 650-653.
123. Cai J., Altes T.A., Miller G.W., et. al.: MR grid-tagging using hyperpolarized helium-3 for regional quantitative assessment of pulmonary biomechanics and ventilation. Magn Reson Med 2007; 58: pp. 373-380.
124. Tustison N.J., Awate S.P., Cai J., et. al.: Pulmonary kinematics from tagged hyperpolarized helium-3 MRI. J Magn Reson Imaging 2010; 31: pp. 1236-1241.
125. Maes F., Collignon A., Vandermeulen D., et. al.: Multimodality image registration by maximization of mutual information. IEEE Trans Med Imaging 1997; 16: pp. 187-198.
126. Wang H., Dong L., O’Daniel J., et. al.: Validation of an accelerated “demons” algorithm for deformable image registration in radiation therapy. Phys Med Biol 2005; 50: pp. 2887-2905.
127. Weruaga L., Morales J., Nez L., et. al.: Estimating volumetric motion in human thorax with parametric matching constraints. IEEE Trans Med Imaging 2003; 22: pp. 766-772.
128. Lu W., Olivera G.H., Chen Q., et. al.: Deformable registration of the planning image (KVCT) and the daily images (MVCT) for adaptive radiation therapy. Phys Med Biol 2006; 51: pp. 4357-4374.
129. Tokuda J., Schmitt M., Sun Y., et. al.: Lung motion and volume measurement by dynamic 3D MRI using a 128-channel receiver coil. Acad Radiol 2009; 16: pp. 22-27.
130. Matsopoulos G.K., Mouravliansky N.A., Asvestas P.A., et. al.: Thoracic non-rigid registration combining self-organizing maps and radial basis functions. Med Image Anal 2005; 9: pp. 237-254.
131. Zijdenbos A.P., Dawant B.M., Margolin R.A., et. al.: Morphometric analysis of white matter lesions in MR images: method and validation. IEEE Trans Med Imaging 1994; 13: pp. 716-724.
132. Jaccard P.: The distribution of flora in the alpine zone. New Phytol 1912; 11: pp. 37-50.
133. Gee J.C., Reivich M., Bajcsy R.: Elastically deforming 3D atlas to match anatomical brain images. J Comput Assist Tomogr 1993; 17: pp. 225-236.
134. Crum W.R., Camara O., Rueckert D., et. al.: Generalised overlap measures for assessment of pairwise and groupwise image registration and segmentation. Med Image Comput Comput Assist Interv 2005; 8: pp. 99-106.
135. Tustison N.J., Gee J.C.: Introducing Dice, Jaccard, and other overlap measures to ITK. Insight J 2009; July-December
136. Liu X, Saboo R, Pizer S, et al. A shape-navigated image deformation model for 4D lung respiratory motion estimation. Presented at: Biomedical Imaging: From Nano to Macro; 2009.
137. Fitzpatrick J.M., West J.B.: The distribution of target registration error in rigid-body point-based registration. IEEE Trans Med Imaging 2001; 20: pp. 917-927.
138. Ehrhardt J, Werner R, Schmidt A-Richberg, et al. Prediction of respiratory motion using a statistical 4D mean motion model. Presented at: Second International Workshop on Pulmonary Image Processing; 2009.
139. Li P., Malsch U., Bendl R.: Combination of intensity-based image registration with 3D simulation in radiation therapy. Phys Med Biol 2008; 53: pp. 4621-4637.
140. Coselmon M.M., Balter J.M., McShan D.L., et. al.: Mutual information based CT registration of the lung at exhale and inhale breathing states using thin-plate splines. Med Phys 2004; 31: pp. 2942-2948.
141. Keall P.J., Joshi S., Vedam S.S., et. al.: Four-dimensional radiotherapy planning for DMLC-based respiratory motion tracking. Med Phys 2005; 32: pp. 942-951.
142. Wu Z., Rietzel E., Boldea V., et. al.: Evaluation of deformable registration of patient lung 4DCT with subanatomical region segmentations. Med Physics 2008; 35: pp. 775-781.
143. Pevsner A., Davis B., Joshi S., et. al.: Evaluation of an automated deformable image matching method for quantifying lung motion in respiration-correlated CT images. Med Phys 2006; 33: pp. 369-376.
144. Sundaram T.A., Gee J.C.: Towards a model of lung biomechanics: pulmonary kinematics via registration of serial lung images. Med Image Anal 2005; 9: pp. 524-537.
145. Liu X., Oguz I., Pizer S.M., et. al.: Shape-correlated deformation statistics for respiratory motion prediction in 4D lung. Medical Imaging 2010; Visualization, Image-Guided Procedures, and Modeling 72010; 625:76252D
146. Sarrut D., Delhay B., Villard P.-F., et. al.: A comparison framework for breathing motion estimation methods from 4-D imaging. IEEE Trans Med Imaging 2007; 26: pp. 1636-1648.
147. Schaefer S., McPhail T., Warren J.: Image deformation using moving least squares.2006.ACMNew York 533–540
148. Plathow C., Schoebinger M., Herth F., et. al.: Estimation of pulmonary motion in healthy subjects and patients with intrathoracic tumors using 3D-dynamic MRI: initial results. Korean J Radiol 2009; 10: pp. 559-567.
149. Plathow C., Fink C., Ley S., et. al.: Measurement of diaphragmatic length during the breathing cycle by dynamic MRI: comparison between healthy adults and patients with an intrathoracic tumor. Eur Radiol 2004; 14: pp. 1392-1399.
150. Segars W.P., Lalush D.S., Tsui B.M.W.: Modeling respiratory mechanics in the MCAT and spline-based MCAT phantoms. IEEE Trans Nucl Sci 2001; 48: pp. 89-97.
151. Hubmayr R.D., Walters B.J., Chevalier P.A., et. al.: Topographical distribution of regional lung volume in anesthetized dogs. J Appl Physiol 1983; 54: pp. 1048-1056.
152. Kaus M.R., Brock K.K., Pekar V., et. al.: Assessment of a model-based deformable image registration approach for radiation therapy planning. Int J Radiat Oncol Biol Phys 2007; 68: pp. 572-580.
153. Kiryu S., Sundaram T., Kubo S., et. al.: MRI assessment of lung parenchymal motion in normal mice and transgenic mice with sickle cell disease. J Magn Reson Imaging 2008; 27: pp. 49-56.
154. Cai J., Sheng K., Benedict S.H., et. al.: Dynamic MRI of grid-tagged hyperpolarized helium-3 for the assessment of lung motion during breathing. Int J Radiat Oncol Biol Phys 2009; 75: pp. 276-284.
155. Sullivan D.C.: Imaging as a quantitative science. Radiology 2008; 248: pp. 328-332.
156. Yoo T.S., Metaxas D.N.: Open science—combining open data and open source software: medical image analysis with the insight toolkit. Med Image Anal 2005; 9: pp. 503-506.
157. Ibanez L, Avila RS, Aylward SR. Open source and open science: how it is changing the medical imaging community. Presented at: Biomedical Imaging: From Nano to Macro; 2006.
158. Kovacevic J.: From the editor-in-chief. IEEE Trans Image Proc 2006; 15: pp. 3625-3626.

Pulmonary Kinematics From Image Data

Normal pulmonary anatomy and physiology

Pulmonary Pathophysiology

Pulmonary Function Testing

Early Studies of Pulmonary Biomechanics

Pulmonary Imaging

Pulmonary kinematics

Deformation Analysis

Intensity-based Estimation of τ From Image Data

Optical Flow

Compressible Optical Flow

A Priori Lung Density Modification

Other Similarity Metrics

Regularization Models and Symmetric Transformation Considerations

Modeling Four-Dimensional Lung Trajectories

Geometric Estimation of τ From Image Data

Landmark Matching

Matching of Curve and Surface Geometric Primitives

MRI Tagging

Validation

Intensity-based Similarity Measures

Overlap Assessment of Anatomic Contours

Expert-defined Landmarks

Miscellaneous Approaches

Public resources

Discussion

Acknowledgment

References

Further Reading

ACR and the Federal Government

Analysis of 2-[Fluorine-18 ] -Fluoro-2-deoxy-D-glucose Uptake Kinetics in PET Studies of Pulmonary Inflammation

Assessment of Pulmonary Hypertension