Rationale and Objectives
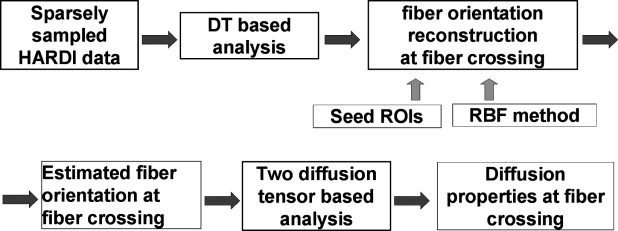
In regions of intravoxel fiber crossing, the single-tensor model does not provide accurate results. The previously published models could resolve this issue but needed a long scan time and long computational time. This article aims to present the new model, which uses interpolated diffusion tensor orientations and requires the estimation of fewer parameters than the previously published model, where all parameters for the two diffusion ellipsoids have to be estimated.
Materials and Methods
Fiber orientation information was reconstructed by using the radial basis function−based interpolation technique from tensor information in given seed regions of interest. Synthetic phantom data were generated, and the proposed method was compared with the conventional two-ellipsoid method. Data from one normal volunteer were analyzed to determine the effectiveness of the proposed method. The number of parameters to be estimated could be reduced by using the estimated fiber orientation information so that diffusion parameter calculation at fiber crossing becomes robust.
Results
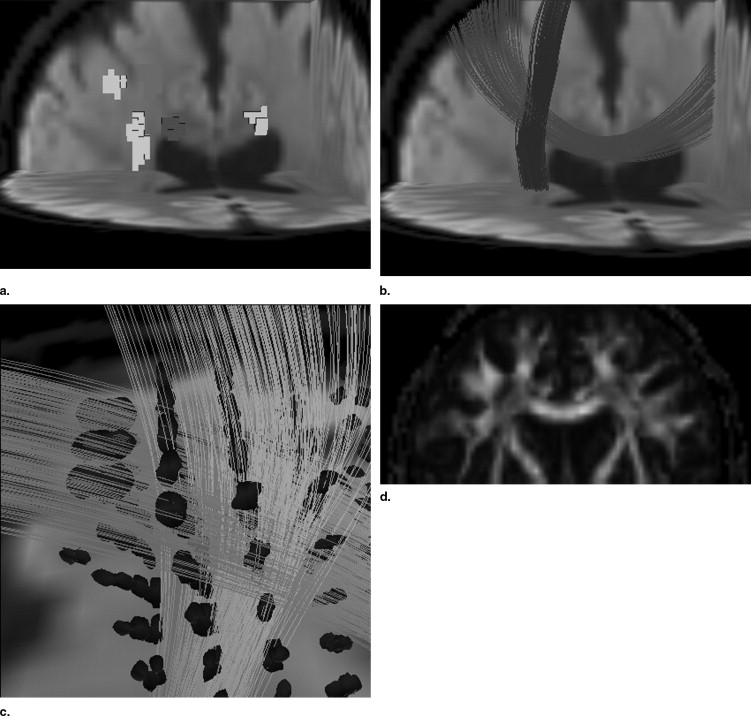
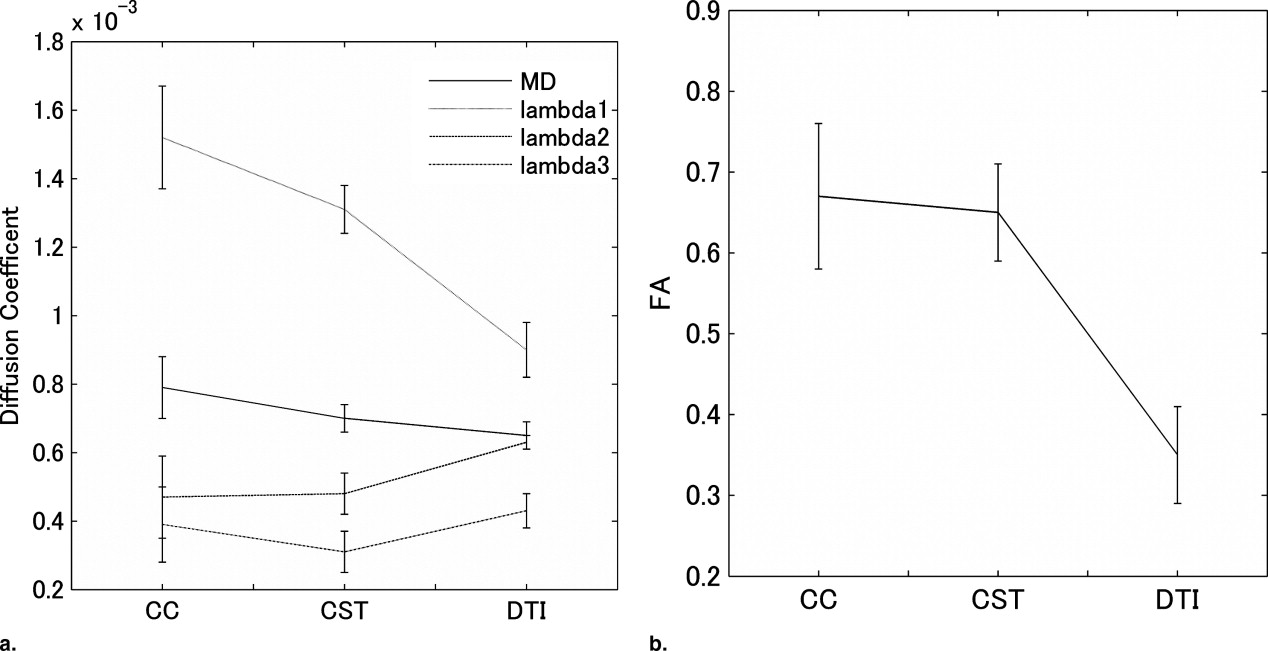
The human study showed that fractional anisotropy (FA) values estimated by the proposed method (FA = 0.67 for the corpus callosum, 0.65 for the corticospinal tract) were significantly higher than that estimated by the standard single-tensor−based method (FA = 0.35), and the estimated FA value showed good agreement with the FA value in the adjacent fiber bundle.
Conclusion
The proposed radial basis function−based technique could reconstruct diffusion properties at the fiber-crossing volume from sparse sampling of high angular diffusion weighted images.
Diffusion tensor imaging (DTI) is a noninvasive and unique magnetic resonance (MR) imaging technique that can measure the microstructural water molecular motion and can evaluate the integrity of the central nerve system. DTI can provide various types of quantitative information regarding water molecular diffusion that include mean diffusivity (MD) and fractional anisotropy (FA). These quantitative indices have been used for multiple sclerosis ( ) and Wallerian degeneration ( ) to assess the white matter integrity and density. Recent advances in diffusion tensor–based tractography (DTT) enabled us to measure diffusion properties along the neuronal fiber tract. The DTT-based quantitative evaluation of the white matter tract demonstrated its clinical usefulness in X-linked adrenoleukodystrophy (X-ALD) ( ), temporal epilepsy ( ), and amyotrophic lateral sclerosis (ALS) ( ).
The DTI technique is based on the assumption that water molecule diffusion underlies the single Gaussian probability distribution model and uses second-order tensor model fit to estimate diffusion property from experimental results ( ). This approximation is widely used for single-fiber bundle but may not be valid for fiber crossing, where two fibers are mixed in a single volume. This partial volume effect distorts the measurement results of diffusion indices, such as pseudo diffusion anisotropy decrease ( ). Inaccurate results may be introduced when the diffusion measurement is performed on the tract across the fiber crossing. To resolve this fiber-crossing issue, precise diffusion measurement techniques and orientation distribution function (ODF) analysis methods have been applied. These techniques include high angular resolution diffusion image (HARDI) measurement ( ) and q-space analysis ( ). However, these techniques require large amounts of diffusion measurement in different orientations or different b values for accurate diffusion property estimation. Typically, an extremely long scan time of greater than 1 hour may be required to acquire the whole data set, so clinical study is limited and the method is mainly applied to excised tissue ( ) or to animals. In addition, q-space technique requires high performance of the gradient system that cannot be achieved with a state-of art clinical MR scanner ( ).
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Materials and methods
Get Radiology Tree app to read full this article<
S(g)=S0∑Ni=1fiexp(−bgDig) S
(
g
)
=
S
0
∑
i
=
1
N
f
i
exp
(
−
b
gD
i
g
)
where S 0 is MR signal when no motion probing gradient was applied, b is the b-value of diffusion acquisition, D is the diffusion tensor of each fiber bundle defined as second-order 3 × 3 tensor, and g represents the motion probing gradient (MPG) orientation vector. The coefficient f i is volume fraction of each fiber bundle that satisfies the equation ∑Ni=1fi=1 ∑
i
=
1
N
f
i
=
1 .
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
s(x)=p(x)+∑Ni=1λi(|x−xi|) s
(
x
)
=
p
(
x
)
+
∑
i
=
1
N
λ
i
(
|
x
−
x
i
|
)
where x represents the location of the point where interpolation is performed, x i represents the position of control point in the specified ROIs, ϕ is the basis function, λ is the weight factor, and p (x) is polynomial function. The basis function ϕ is a real valued function on [0, ∞ ∞ ], and well-known choices of the radial basis function include the thin-plate spline, Gaussian, biharmonic, and triharmonic. We used triharmonic radial basis function in this study.
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
S=S0(f1exp(−bD1)+(1−f1)exp(−bD2)) S
=
S
0
(
f
1
exp
(
−
b
D
1
)
+
(
1
−
f
1
)
exp
(
−
b
D
2
)
)
where D 1 and D 2 are the diffusion tensors and f 1 is volume fraction of first tensor. We defined three eigenvectors of two diffusion tensors as u→1,u→2,u→3 u
→
1
,
u
→
2
,
u
→
3 for D 1 and v→1,v→2,v→3 v
→
1
,
v
→
2
,
v
→
3 for D 2 . When ssHARDI were acquired with MPG orientation vectors (g→1,g→2,…….,g→n) (
g
→
1
,
g
→
2
,
…….
,
g
→
n
) , MR signal from the fiber crossing in the two-ellipsoid model can be described as follows.
S=S0(f1exp(−b(λu1g2u1+λu2g2u2+λu3g2u3))+(1−f1)exp(−b(λv1g2v1+λv2g2v2+λv3g2v3))) S
=
S
0
(
f
1
exp
(
−
b
(
λ
u
1
g
u
1
2
+
λ
u
2
g
u
2
2
+
λ
u
3
g
u
3
2
)
)
+
(
1
−
f
1
)
exp
(
−
b
(
λ
v
1
g
v
1
2
+
λ
v
2
g
v
2
2
+
λ
v
3
g
v
3
2
)
)
)
where g un is the projection of g onto the eigenvector u or v and λ ui , λ vi are the eigenvalues correspond to the eigenvectors u i and v i . Consequently, in the proposed two-ellipsoid model with interpolation of tract orientation, seven unknown parameters need to be estimated. These seven parameters include the eigenvalues of two–diffusion tensor ellipsoids and volume fraction of the tensors. The optimum tensor parameters in multiple tensors are determined as minimizing the error between the acquired ssHARDI data and the model. Simplex method ( ) was used to find the optimum values.
Get Radiology Tree app to read full this article<
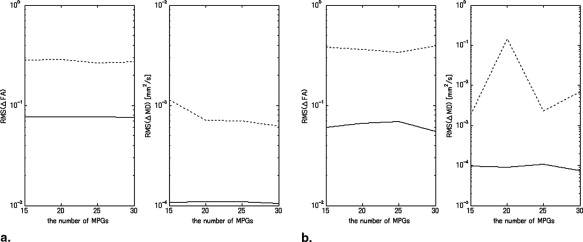
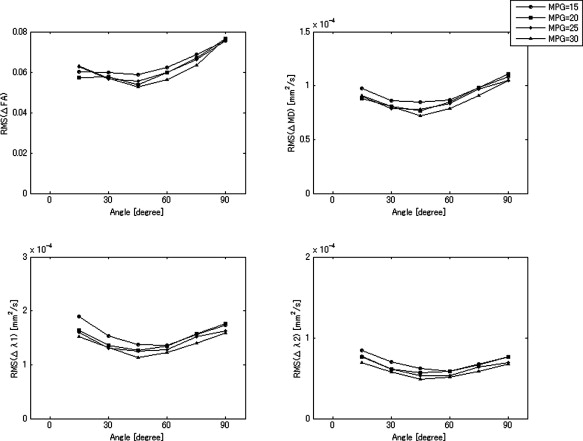
Numerical Phantom Study
Get Radiology Tree app to read full this article<
Human Study
Get Radiology Tree app to read full this article<
Results
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Discussion
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
Get Radiology Tree app to read full this article<
References
1. Werring D.H., Clark C.A., Barker G.J., Thompson A.J., Miller D.H.: Diffusion tensor imaging of lesions and normal-appearing white matter in multiple sclerosis. Neurology 1999; 52: pp. 1626-1632.
2. Werring D.J., Clark C.A., Barker G.J., et. al.: The structural and functional mechanisms of motor recovery: Complementary use of diffusion tensor and functional magnetic resonance imaging in a traumatic injury of the internal capsule. J Neurol Neurosurg Psychiatry 1998; 65: pp. 863-869.
3. Dubey P., Fatemi A., Huang H., et. al.: Diffusion tensor–based imaging reveals occult abnormalities in adrenomyeloneuropathy. Ann Neurol 2005; 58: pp. 758-766.
4. Concha L., Beaulieu C., Gross D.W.: Bilateral limbic diffusion abnormalities in unilateral temporal lobe epilepsy. Ann Neurol 2005; 57: pp. 188-196.
5. Aoki S., Iwata N.K., Masutani Y., et. al.: Quantitative evaluation of the pyramidal tract segmented by diffusion tensor tractography: Feasibility study in patients with amyotrophic lateral sclerosis. Radiation Medicine 2005; 23: pp. 195-199.
6. Basser P.J., Pierpaoli C.: Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J Magn Reson B 1996; 111: pp. 209-219.
7. Alexander A.L., Hasan K.M., Lazar M., Tsuruda J.S., Parker D.L.: Analysis of partial volume effects in diffusion-tensor MRI. Magn Reson Med 2001; 45: pp. 770-780.
8. King M.D., Houseman J., Roussel S.A., van Bruggen N., Williams S.R., Gadian D.G.: q-Space imaging of the brain. Magn Reson Med 1994; 32: pp. 707-713.
9. Tuch D.S., Reese T.G., Wiegell M.R., Makris N., Belliveau J.W., Wedeen V.J.: High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magn Reson Med 2002; 48: pp. 577-582.
10. Assaf Y., Mayk A., Cohen Y.: Displacement imaging of spinal cord using q-space diffusion-weighted MRI. Magn Reson Med 2000; 44: pp. 713-722.
11. Peter J.: Basser. Magn Reson Med 2002; 47: pp. 392-397.
12. Kreher B.W., Schneider J.F., Mader I., Martin E., Hennig J., Il’yasov K.A.: Multitensor approach for analysis and tracking of complex fiber configurations. Magn Reson Med 2005; 54: pp. 1216-1225.
13. Mori S., Crain B.J., Chacko V.P., van Zijl P.C.: Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol 1999; 45: pp. 265-269.
14. Masutani Y., Aoki S., Abe O., Hayashi N., Otomo K.: MR diffusion tensor imaging: Recent advance and new techniques for diffusion tensor visualization. Eur J Radiol 2003; 46: pp. 53-66.
15. Savchenko V.V., Pasko A.A., Okunev O.G., Kunii T.L.: Function representation of solids reconstructed from scattered surface points and contours. Computer Graphics Forum 1995; 14: pp. 181-188.
16. Lagarias J.C., Reeds J.A., Wright M.H., Wright P.E.: Convergence properties of the Nelder-Mead simplex method in low dimensions. SIAM J Optimiz 1998; 9: pp. 112-147.
17. Jones D.K., Horsfield M.A., Simmons A.: Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn Reson Med 1999; 42: pp. 515-525.
18. Mangin J.F., Poupon C., Clark C., Le Bihan D., Bloch I.: Distortion correction and robust tensor estimation for MR diffusion imaging. Med Image Anal 2002; 6: pp. 191-198.
19. Jones D.K., Basser P.J.: “Squashing peanuts and smashing pumpkins”: How noise distorts diffusion-weighted MR data. Magn Reson Med 2004; 52: pp. 979-993.
20. Jones D.K.: The effect of gradient sampling schemes on measures derived from diffusion tensor MRI: A Monte Carlo study. Magn Reson Med 2004; 51: pp. 807-815.
21. Tuch D.S.: Q-ball imaging. Magn Reson Med 2004; 52: pp. 1358-1372.
22. Assaf Y., Basser P.J.: Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain. Neuroimage 2005; 27: pp. 48-58.
23. Batchelor P.G., Atkinson D., Hill D.L., Calamante F., Connelly A.: Anisotropic noise propagation in diffusion tensor MRI sampling schemes. Magn Reson Med 2003; 49: pp. 1143-1151.
24. Skare S., Hedehus M., Moseley M.E., Li T.Q.: Condition number as a measure of noise performance of diffusion tensor data acquisition schemes with MRI. J Magn Reson 2000; 147: pp. 340-352.