Home Segmentation of Brain MRI in Young Children
Post
Cancel

Segmentation of Brain MRI in Young Children

Posted Oct 31, 2007 Updated Apr 7, 2023
By Maria Murgasova , Leigh Dyet , David Edwards , Mary Rutherford , Jo Hajnal , Daniel Rueckert
10 min read

Rationale and Objectives

This article deals with an automatic tissue segmentation of brain magnetic resonance imaging (MRI) in young children.

Materials and Methods

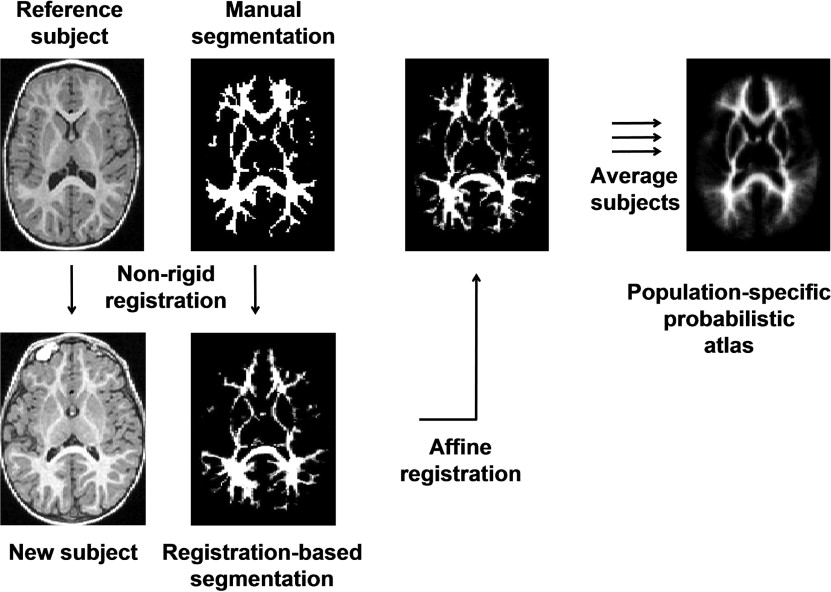
We examine the suitability of state-of-the-art methods developed for the adult brain when applied to the segmentation of the brain MRI in young children. We develop a method of creation of a population-specific atlas in young children using a single manual segmentation. The method is based on nonlinear propagation of the segmentation into population and subsequent affine alignment into a reference space and averaging.

Results

Using this approach, we significantly improve the performance of the popular expectation-maximization algorithm on brain MRI in young children. The method can be used for building probabilistic atlases with any number of structures. We compare resulting algorithm with nonrigid registration-based label propagation.

Conclusions

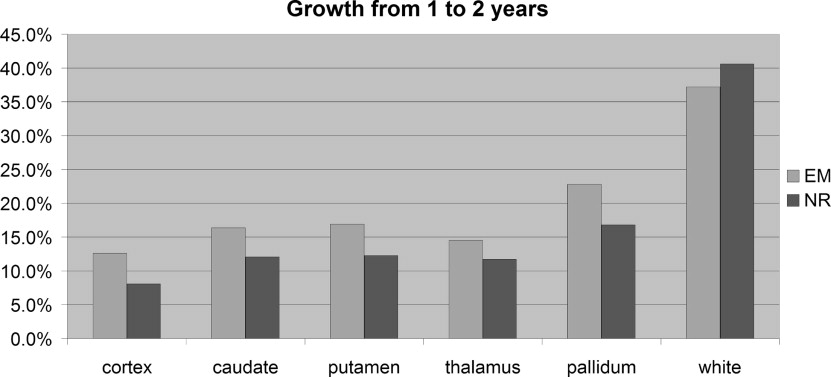
Finally, both methods are used to measure the volume of seven brain structures and measure the growth between 1 and 2 years of age.

The problem of automatic segmentation of brain magnetic resonance imaging (MRI) has been extensively studied in past decade thanks to its applications in clinical studies of normal and diseased brain. Recent research of brain development in prematurely born children requires reliable and accurate automatic segmentation techniques for the neonatal and early childhood brain as well. Approximately 40% of prematurely born children have cognitive, neurologic, or behavioral impairment ( ); the cerebral abnormalities underlying problems such as minor motor impairment or inattention still remain unclear. Accurate tissue quantification of the preterm brain in early childhood would allow us to study the growth of different structures and help to relate developmental outcomes to changes in volume and shape of anatomic structures.

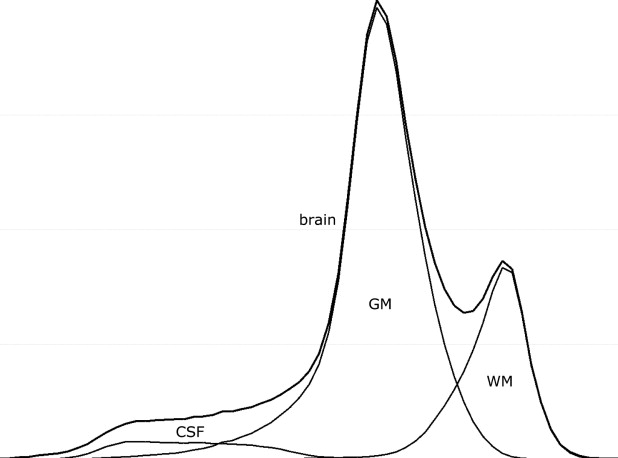
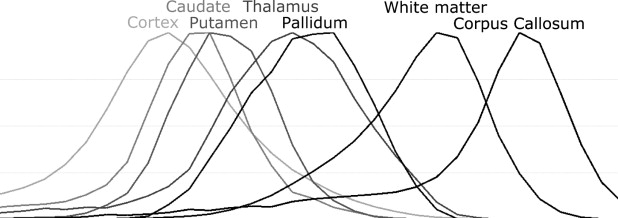
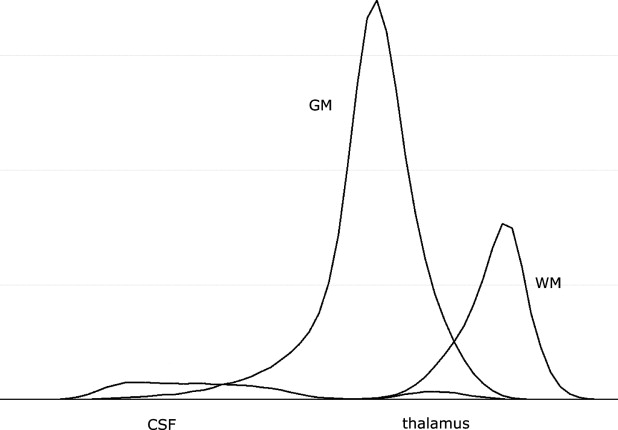
In addition to noise, intensity nonuniformity, partial volume effect, and natural tissue intensity variation present in the adult brain MRI, neonatal and infant brain MRI tissue intensities have even greater natural variation caused by ongoing process of myelination of white matter. This is most profound in neonates in whom white matter is extremely difficult to distinguish from gray matter on T1-weighted MRI sequences. By the age of 1 or 2 years, the majority of white matter has myelinated. However, the natural tissue intensity distribution overlap may result in large misclassifications in central brain structures when using intensity-based segmentation approaches. This problem is further compounded by the fact that a child’s brain differs significantly in size and shape from the adult brain, in particular in the central structures of the brain ( ). This causes problems for methods which rely on probabilistic atlases built from adults as spatial prior information.

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Figure 1, Intensity distribution of the whole brain, white matter, gray matter, and cerebrospinal fluid.

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Figure 2, Real tissue distribution of different brain structures based on manual segmentation of a 2-year-old child brain magnetic resonance imaging. Corpus callosum is a central brain white matter structure with significantly higher intensities than general white matter. Deep gray matter structures pallidum, thalamus, putamen, and caudate are brighter than cortical gray matter.

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

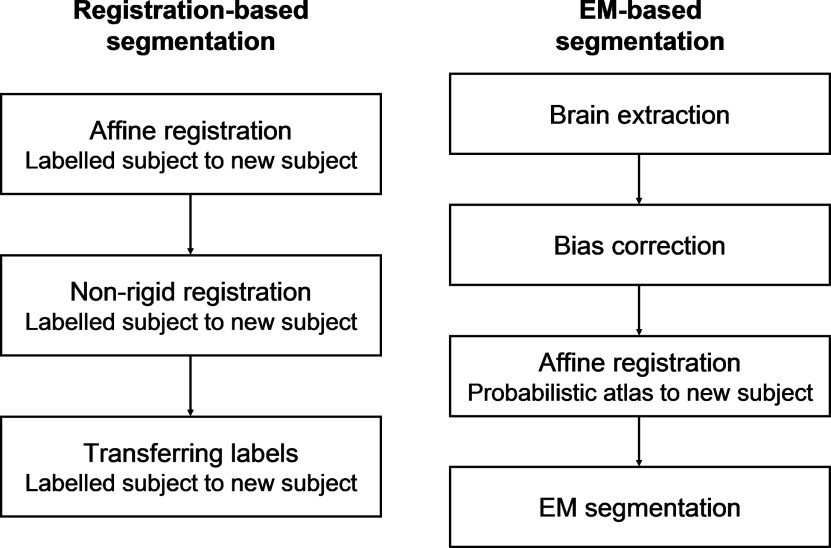
Segmentation methods

Registration-Based Segmentation

Get Radiology Tree app to read full this article<

Figure 3, Registration: (a) the reference image; (b) nonrigid registration of the reference image to the new image; (c) the new image; (d) affine registration of the reference image to the new image; (e) nonrigid registration-based segmentation of white matter; and (f) manual segmentation of white matter.

Figure 4, Segmentation pipeline for registration-based and expectation-maximization algorithm–based approaches.

Get Radiology Tree app to read full this article<

EM-Based Segmentation

Get Radiology Tree app to read full this article<

Figure 6, Expectation-maximization algorithm segmentation into three tissue classes: (a) the image; (b) hard segmentation. Soft segmentation: (c) white matter (WM); (d) gray matter; and (e) cerebrospinal fluid. Compare with results of registration-based segmentation of WM ( Fig 3 e) and manual segmentation of WM ( Fig 3 f).

Figure 5, The probabilistic atlas created from population of 2-year-old children.

Get Radiology Tree app to read full this article<

E-Step

Get Radiology Tree app to read full this article<

pmik=G(yi,μm−1k,σm−1k)patlasik∑jG(yi,μm−1j,σm−1j)patlasij p

i

k

m

=

G

(

y

i

,

μ

k

m

−

1

,

σ

k

m

−

1

)

p

i

k

a

t

l

a

s

∑

j

G

(

y

i

,

μ

j

m

−

1

,

σ

j

m

−

1

)

p

i

j

a

t

l

a

s

Get Radiology Tree app to read full this article<

M-Step

Get Radiology Tree app to read full this article<

μmik=∑ipmikyi∑ipmikσmk=∑ipmik(yi−μmk)2∑ipnik μ

i

k

m

=

∑

i

p

i

k

m

y

i

∑

i

p

i

k

m

σ

k

m

=

∑

i

p

i

k

m

(

y

i

−

μ

k

m

)

2

∑

i

p

i

k

n

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

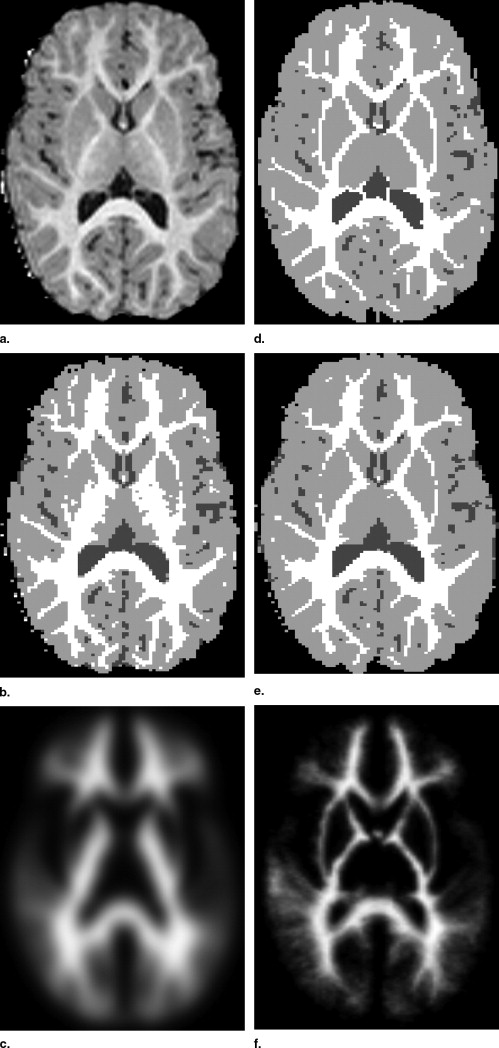
Prior information for EM segmentation

Standard Probabilistic Atlas

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Figure 7, Misclassification in thalamus: substantial amount of subcortical grey matter classified as white. (a) Magnetic resonance image of a 2-year-old brain; (b) expectation-maximization algorithm (EM) segmentation using the adult atlas; (c) EM segmentation using the 2-year-old child atlas; and (d) manual segmentation.

Figure 8, Histogram of the tissue intensity probability distribution for white matter (WM), gray matter (GM), cerebrospinal fluid (CSF) and thalamus (a subcortical GM structure) based on a manual segmentation of brain magnetic resonance imaging from a 2-year-old child. Distributions of GM and CSF differ significantly from the Gaussian distribution from partial volume effect. The intensity distribution of thalamus lies in the region of the overlap of the WM and GM distributions.

Get Radiology Tree app to read full this article<

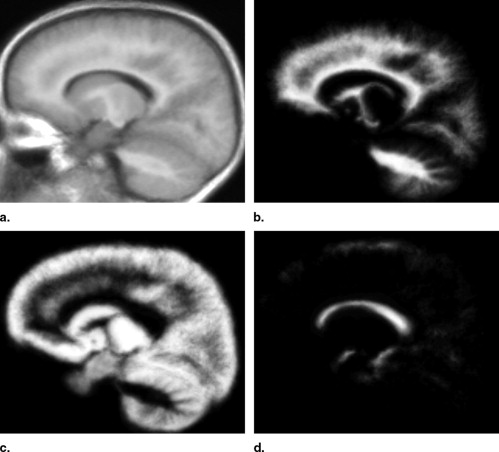
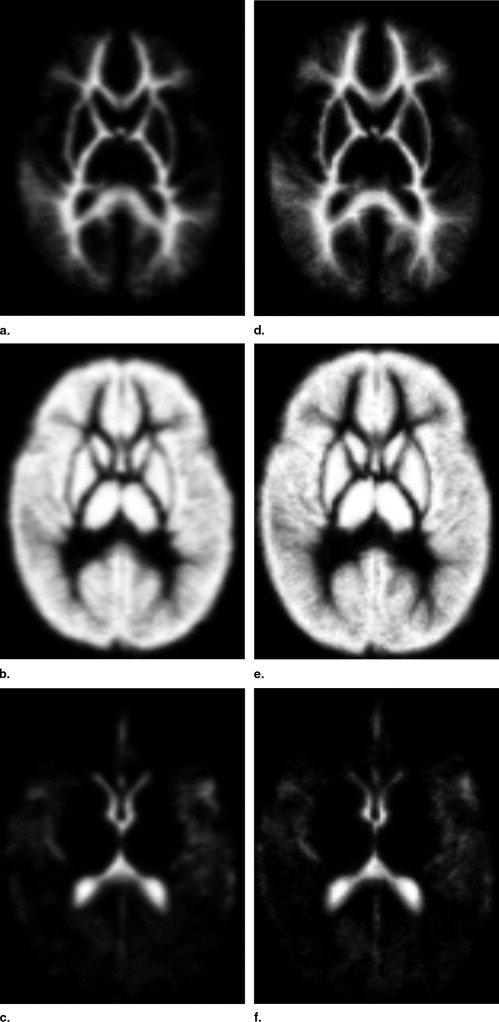
Creating a Population-Specific Atlas for EM Segmentation

Get Radiology Tree app to read full this article<

Figure 9, Creating a population-specific atlas. A single manual segmentation is transferred to a population of subjects by nonrigid registration. All the segmentations are then aligned with the reference subject with affine registration and averaged.

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Figure 10, The comparison of the probabilistic atlases created from population of 1-year old children (first column) and 2-year-old children (second column).

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Figure 11, Improvement of segmentation using our new atlas: (a) magnetic resonance image of a 2-year-old brain; (b) segmentation using standard MNI brain atlas; (c) standard MNI brain atlas; (d) manual segmentation; (e) segmentation using our 2-year-old brain atlas; and (f) our 2-year-old brain atlas.

Get Radiology Tree app to read full this article<

Comparison of the methods

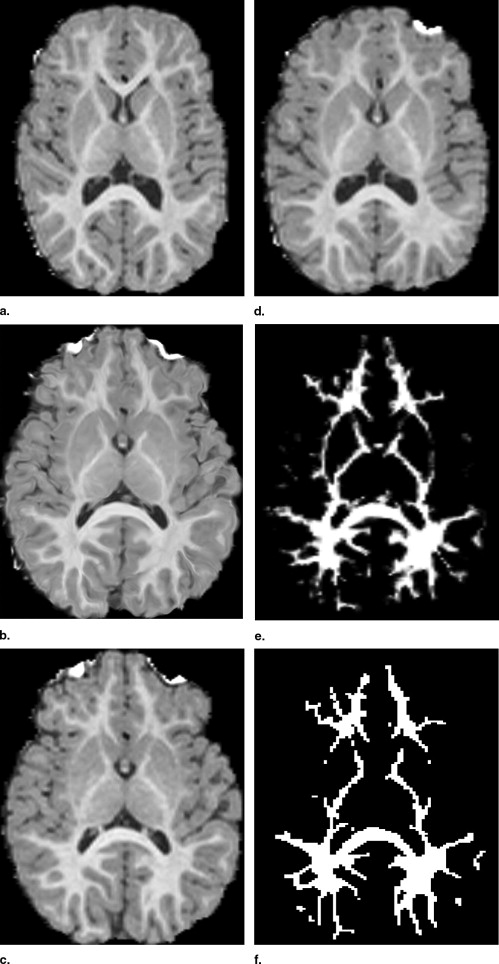
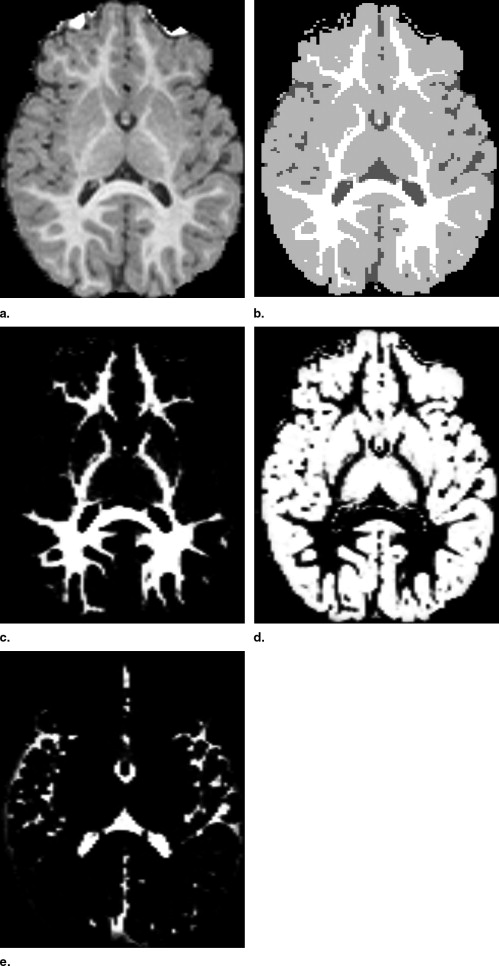
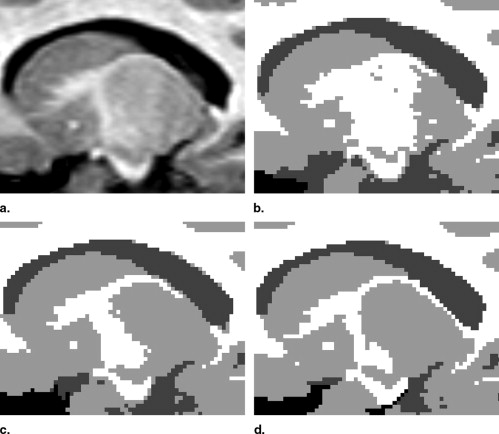
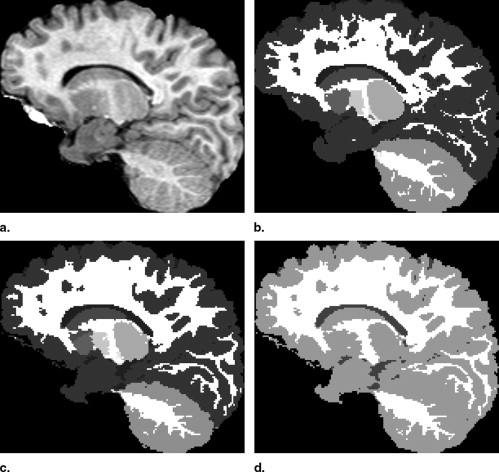
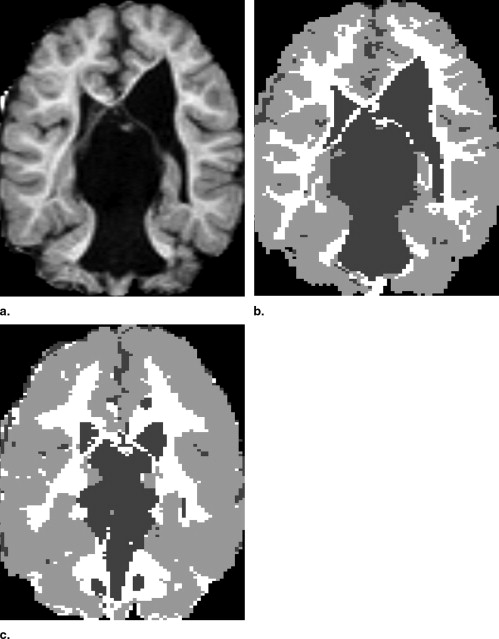
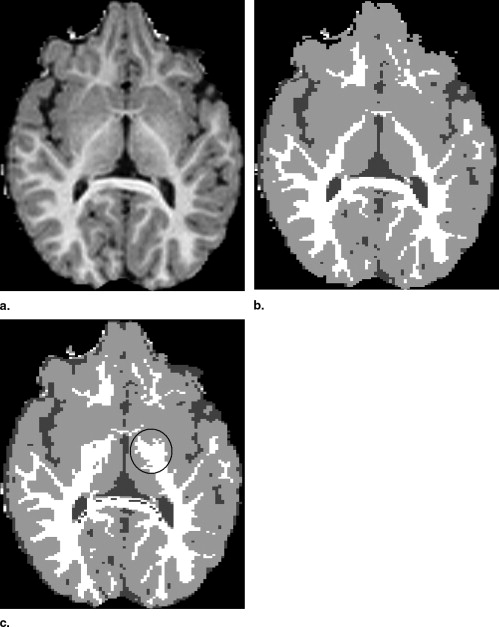
Visual Inspection

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Figure 12, Segmentation of brain magnetic resonance imaging in 2-year-old child: (a) the image; (b) registration-based segmentation into 11 structures; (c) expectation-maximization algorithm (EM)-based segmentation into 11 structures; and (d) EM-based segmentation into three structures.

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Figure 13, Segmentation of brain magnetic resonance imaging in a 2-year-old child with focal lesions: (a) the image; (b) registration-based segmentation into three structures after removing brainstem and cerebellum; and (c) failed expectation-maximization algorithm–based segmentation into three structures.

Get Radiology Tree app to read full this article<

Influence of Population-Specific Atlas on EM-Based Segmentation into WM, GM, and CSF

Get Radiology Tree app to read full this article<

Table 3

Average Validation Results of EM-Based Method With Population-Specific Atlas and Nonrigid Registration-Based Label Propagation on Four 2-Year-Old Subjects Using Dice Metrics

Method White Cortex Caudate Thalamus EM 2-year atlas 0.87 0.87 0.84 0.86 NR registration 0.84 0.83 0.86 0.89

EM: our implementation of expectation-maximization algorithm; NR: non-rigid registration-based segmentation.

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

D=2∗|Tgt∩Tseg||Tgt|+|Tseg| D

=

2

∗

|

T

g

t

∩

T

s

e

g

|

|

T

g

t

|

+

|

T

s

e

g

|

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

D=2∗∣∣Tthalgt∩TGMseg∣∣∣∣Tthalgt∣∣+∣∣TGMseg∩Tthakgt∣∣ D

=

2

∗

|

T

g

t

t

h

a

l

∩

T

s

e

g

G

M

|

|

T

g

t

t

h

a

l

|

+

|

T

s

e

g

G

M

∩

T

g

t

t

h

a

k

|

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Table 1

Performance of the Segmentation Methods on a Single 2-Year-Old Subject

Method White Matter Gray Matter Cerebrospinal Fluid EMS 0.84 0.88 0.69 EMS-Markov random fields 0.85 0.89 0.62 EM adult atlas 0.85 0.88 0.68 EM 2-year atlas 0.88 0.92 0.78

EMS: expectation maximization segmentation with bias correction ( ); EM: our implementation of EMS without bias correction.

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Table 2

Average Validation Results EM Segmentation on Four 2-Year-Old Subjects Using Dice Metrics

Method White Matter Gray Matter Thalamus EM 2-year atlas 0.86 0.88 0.92 EM adult atlas 0.84 0.86 0.70

EM: our implementation of EMS without bias correction.

Get Radiology Tree app to read full this article<

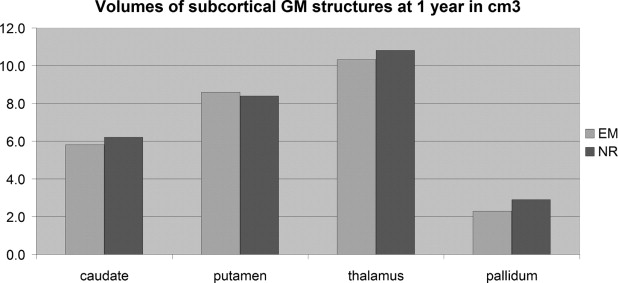
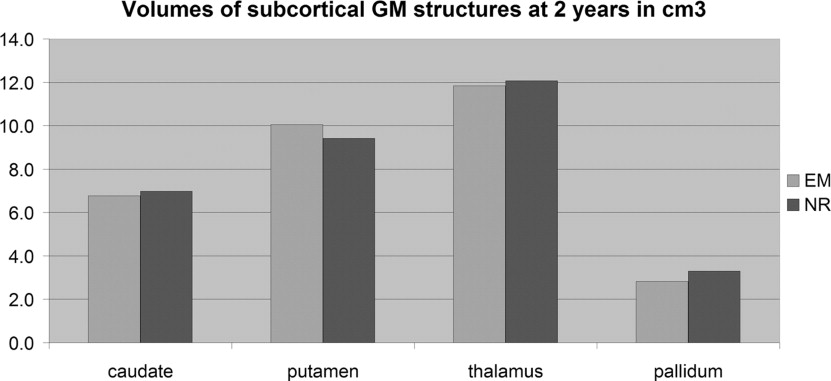
Comparison of EM-Based and Registration-Based Segmentation into Seven Structures

Get Radiology Tree app to read full this article<

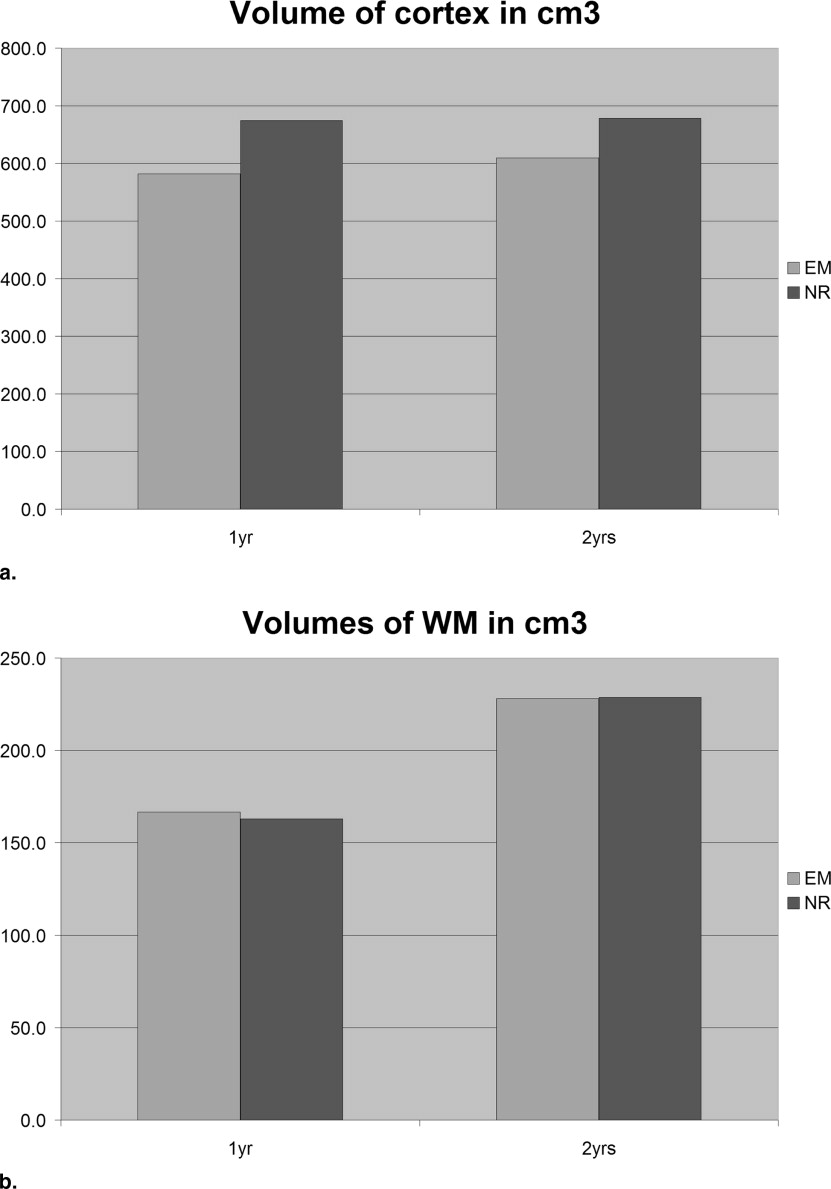
Calculating Brain Growth From 1 to 2 Years

Get Radiology Tree app to read full this article<

Figure 14, Average volumes of cortex and white matter calculated from 16 subjects at 1 and 2 years.

Figure 15, Average volumes of subcortical gray matter structures calculated from 16 subjects at 1 year.

Figure 16, Average volumes of subcortical gray matter structures calculated from 16 subjects at 2 years.

Figure 17, Average growth of brain structures from 1 to 2 years calculated from 16 subjects.

Get Radiology Tree app to read full this article<

Discussion

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Get Radiology Tree app to read full this article<

Figure 18, (a) Brain magnetic resonance imaging of a 2-year-old child. Soft segmentation of white matter (WM); (b) expectation maximization segmentation with population-specific atlas; and (c) statistical parametric mapping 5 with nonrigidly aligned standard adult atlas. Parts of thalamus and pallidum are misclassified as WM (area in black circle).

Get Radiology Tree app to read full this article<

Conclusion

Get Radiology Tree app to read full this article<

References

  • 1. Marlow N., Wolke D., Bracewell M.A., et. al., EPICure Study Group: Neurologic and developmental disability at six years of age after extremely preterm birth. Pediatrics 2005; 115: pp. 286-294.

  • 2. Wilke M., Schmithorst V., Holland S.: Normative pediatric brain data for spatial normalization and segmentation differs from standard adult data. Magn Res Med 2003; 50: pp. 749-757.

  • 3. Leemput K.V., Maes F., Vandermeulen D., et. al.: Automated model-based tissue classification of MR images of the brain. IEEE Trans Med Imaging 1999; 18: pp. 897-908.

  • 4. Leemput K.V., Maes F., Vandermeulen D., et. al.: Automated model-based bias field correction of MR images of the brain. IEEE Trans Med Imaging 1999; 18: pp. 885-896.

  • 5. Rueckert D., Sonoda L.I., Hayes C., et. al.: Non-rigid registration using free-form deformations: application to breast MR images. IEEE Trans Med Imaging 1999; 18: pp. 712-721.

  • 6. Wells W.M., Grimson W.E.L., Kikinis R., et. al.: Adaptive segmentation of MRI data. IEEE Trans Med Imaging 1996; 15: pp. 429-442.

  • 7. Ashburner J.: Computational neuroanatomy.2000.University College London

  • 8. Ashburner J., Friston K.: Unified segmentation. NeuroImage 2005; 26: pp. 839-851.

  • 9. Zhang Y., Brady M., Smith S.: Segmentation of brain MR images through a hidden Markov random field model and the expectation maximization algorithm. IEEE Trans Med Imaging 2001; 20: pp. 45-57.

  • 10. Fischl B., Salat D., Busa E., et. al.: Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neurotechnique 2002; 33: pp. 341-355.

  • 11. Ren J., Sneller B., Rueckert D., et. al.: A comparison of tissue type labelings of direct classification and segmentation propagation techniques for MR brain images. Proc Med Image Understanding Anal 2005; pp. 55-58.

  • 12. Pohl K., Wells W., Guimond A., et. al.: Incorporating non-rigid registration into expectation maximization algorithm to segment MR images. Proc 5th Int Conf Med Image Comp Computer-Assisted Intervention 2002; 2488: pp. 564-572.

  • 13. D’Agostino E., Maes F., Vandermeulen D., et. al.: Non-rigid atlas-to-image registration by minimization of class-conditional image entropy. Proc 7th Int Conf Med Image Comp Computer-Assisted Intervention 2004; pp. 745-753.

  • 14. Pohl K.: Prior information for brain parcellation.2005.Massachusetts Institute of Technology

  • 15. Pohl K.M., Fisher J., Grimson W., et. al.: A Bayesian model for joint segmentation and registration. NeuroImage 2006; 31: pp. 228-239.

  • 16. Cocosco C.A., Zijdenbos A.P., Evans A.C.: A fully automatic and robust brain MRI tissue classification method. Med Image Anal 2003; 7: pp. 513-527.

  • 17. Prastawa M., Gilmore J.H., Lin W., et. al.: Automatic segmentation of neonatal brain MRI. Proc 7th Int Conf Med Image Comp Computer-Assisted Intervention 2004; pp. 10-17.

  • 18. Hajnal J., Hill D., Hawkes D.: Medical image registration.2001.CRC Press UCUSA

  • 19. Dempster A.P., Laird N.M., Rubin D.B.: Maximum likelihood from incomplete data via the EM-algorithm. J Roy Stat So 1977; 39: pp. 1-38.

  • 20. UCL/SPM. Statistical parametric mapping. Available online at: www.fil.ion.ucl.ac.uk/spm .

  • 21. Sled J.G., Zijdenbos A., Evans A.: A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans Med Imaging 1998; 17: pp. 87-97.

  • 22. Smith S.: Fast robust automated brain extraction. Human Brain Map 2002; 17: pp. 143-155.

  • 23. Expectation maximization segmentation. Available online at: www.medicalimagecomputing.com/downloads/ems.php .

  • 24. Dice L.R.: Measures of the amount of ecologic association between species. Ecology 1945; 26: pp. 297-302.

  • 25. Image Registration Toolkit. Available online at: www.doc.ic.ac.uk/∼dr/software/ .

  • 26. Crum W.R., Rueckert D., Jenkinson M., et. al.: A framework for detailed objective comparison of non-rigid registration algorithms in neuroimaging. MICCAI 2004; 1: pp. 679-686.

Academic Radiology, Volume 14, Issue 11
Journals General Radiology
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Contents