Statistical Approaches for Modeling Radiologists' Interpretive Performance

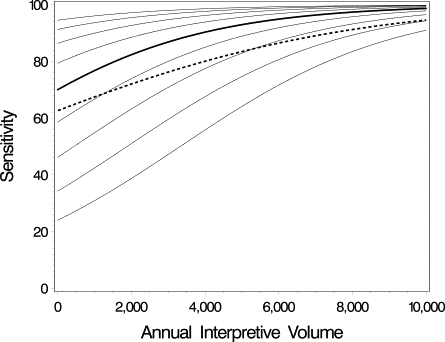
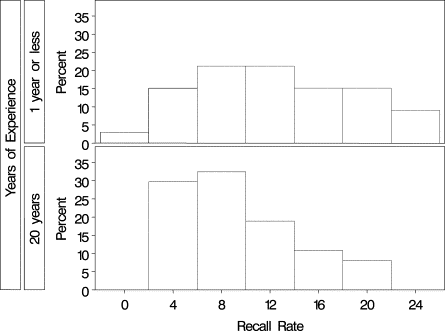
Although much research has been conducted to understand the influence of interpretive volume on radiologists’ performance of mammography interpretation, the published literature has been unable to achieve consensus on the volume standards required for optimal mammography accuracy. One potential contributing factor is that studies have used different statistical approaches to address the same underlying scientific question. Such studies have relied on multiple mammography interpretations from a sample of radiologists; thus, an important statistical issue is appropriately accounting for dependence, or correlation, among interpretations made by (or clustered within) the same radiologist. The aim of this review is to increase awareness about differences between statistical approaches used to analyze clustered data. Statistical frameworks commonly used to model binary measures of interpretive performance are reviewed, focusing on two broad classes of regression frameworks: marginal and conditional models. Although both frameworks account for dependence in clustered data, the interpretations of their parameters differ; hence, the choice of statistical framework may (implicitly) dictate the scientific question being addressed. Additional statistical issues that influence estimation and inference are also discussed, together with their potential impact on the scientific interpretation of the analysis. This work was motivated by ongoing research being conducted by the National Cancer Institute’s Breast Cancer Surveillance Consortium; however, the ideas are relevant to a broad range of settings in which researchers seek to identify and understand sources of variability in clustered binary outcomes.

Despite improvements in the technical quality of mammography since the implementation of the Mammography Quality Standards Act of 1992 ( ), radiologists’ interpretive performance in mammography has remained highly variable in the United States ( ). Much research has been conducted toward understanding the role of patient, radiologist, and facility characteristics in explaining this variation ( ). Notwithstanding this large body of work, substantial unexplained variability in interpretative performance remains.

A recent topic of interest is evaluating the influence of radiologists’ annual mammography interpretive volume on performance, which could help inform whether current certification requirements should be changed ( ). Conflicting study findings, however, have defied consensus on whether and how interpretive volume influences performance ( ). Although these studies shared the common goal of understanding the influence of volume on performance, they differed in several important ways, including the study populations, time frames, choices of performance indexes used as the primary outcomes, definitions of interpretive volume, and selection of adjustment variables. Studies also differed in the statistical approaches and modeling strategies used to characterize and estimate the associations of interest. To achieve consensus on the answer to a specific scientific question, such as the influence of interpretive volume on interpretative performance, it is important to place into context differences in statistical methodologies and how they may influence results. A recent Institute of Medicine ( ) report on improving breast imaging quality standards underscored the need “to establish the implications, advantages, and disadvantages of statistical approaches to evaluating the influence of volume on interpretive performance.”

Motivated by this, we review commonly used statistical approaches for modeling the influence of radiologist characteristics on interpretive performance. Evaluating radiologists’ interpretive performance relies on observing multiple interpretations for each radiologist. These data are often referred to as repeated-measures or clustered data, because outcomes (ie, interpretations) are clustered within the interpreting radiologist. Although researchers have a broad range of statistical methods at their disposal for analyzing clustered data, the focus here is on regression-based modeling approaches, because they permit adjustment for possible differences in case mix shown to affect interpretive performance ( ). Two broad classes of regression model formulations have been used to study interpretive performance: marginal and conditional models. We compare and contrast these approaches, focusing on the scientific interpretation of their parameters. We also outline various scientific and statistical issues that should be considered when deciding on the specific modeling approach to use or when interpreting the results of an analysis. We emphasize that the choice of the statistical method may (often implicitly) dictate the scientific question being addressed and that modeling assumptions, and violations of these assumptions, have important implications for achieving consensus across studies that have a common scientific goal.

Throughout this paper, we illustrate concepts using mammography interpretive performance data collected by the Breast Cancer Surveillance Consortium (BCSC) ( ). Funded by the National Cancer Institute, the BCSC is a consortium of seven mammography registries that has collected information on 7.5 million mammographic examinations interpreted by more than 1,000 radiologists at 243 radiology facilities in seven states across the United States ( http://breastscreening.cancer.gov ). Each mammography registry annually links women in the registry to a state tumor registry or regional Surveillance Epidemiology and End Results program that collects population-based cancer data. Five of the seven registries also link to pathology databases to supplement cancer registry information and collect information about benign disease. All data are sent to the BCSC’s central Statistical Coordinating Center (SCC) for pooled analysis. Each BCSC registry, as well as the SCC, received institutional review board approval either for active or passive consenting processes or for a waiver of consent to enroll women who obtained mammograms at BCSC sites, to link data, and to perform analytic studies. All procedures are compliant with the Health Insurance Portability and Accountability Act, and all registries and the SCC received federal certificates of confidentiality that protect the identities of research subjects, including radiologists ( ).

The remainder of this paper is organized as follows. We begin by outlining some design considerations, concentrating on issues associated with the choice of primary outcomes and predictor definitions. We then provide an overview of marginal and conditional models and discuss differences in the interpretation of their model parameters. We give a brief description of additional statistical issues that will often be encountered in the analysis of clustered binary data and conclude with a discussion and some recommendations for analytic strategies. Although this paper is motivated by challenges in modeling the interpretive performance of mammography, the ideas are relevant to a broad range of settings in which researchers seek to understand sources of variability in clustered binary outcomes, beyond both mammography and radiologists’ interpretive performance.

Design considerations

Get Radiology Tree app to read full this article<

Choice of Outcome

Get Radiology Tree app to read full this article<

Choice of Predictor

Get Radiology Tree app to read full this article<

Separation of Between-cluster and Within-cluster Predictor Effects

Get Radiology Tree app to read full this article<

logitπ(Xij)=β0+Xijβ1. logit

(

)

Get Radiology Tree app to read full this article<

logitπ(Xij)=β*0+Xi¯¯¯¯βb1+(Xij−Xi¯¯¯¯)βw1. logit

(

)

(

−

)

Get Radiology Tree app to read full this article<

Regression approaches for clustered data

Get Radiology Tree app to read full this article<

Conditional or Cluster-specific Models

Get Radiology Tree app to read full this article<

logitπC(Xij,bi)=βC0+Xij,1βC1+⋅⋅⋅Xij,pβCp+bi, logit

(

)

⋅

where b__i is a radiologist-specific parameter, and π C ( X__ij , b__i ) is the conditional probability of recall given the covariates X__ij = ( X__ij ,1 , …, X__ij , p ) and the radiologist-specific parameter b__i . Intuitively, the radiologist-specific effect b__i induces dependence across the multiple observations from the i th radiologist, because a large positive value of b__i indicates that each mammogram-specific probability of being recalled, given by Equation 3 , will be high, whereas a large negative value of b__i indicates that each mammogram-specific probability of recall will be low. In more general conditional models, the single radiologist-specific effect b__i can be replaced with a vector of effects, potentially depending on observed covariates.

Get Radiology Tree app to read full this article<

Marginal or Population-averaged Models

Get Radiology Tree app to read full this article<

logitπM(Xij)=βM0+Xij,1βM1+⋅⋅⋅+Xij,pβMp. logit

(

)

⋅

Get Radiology Tree app to read full this article<

U(βM)=∑Ni=1DTiV−1i[Yi−πM(Xi)]=0, U

(

)

∑

−

[

−

(

)

]

where Di is the first derivative of the vector π M ( Xi ) with respect to the regression parameters β M , and Vi is the assumed variance-covariance matrix for the vector of observed outcomes for the i th radiologist Yi . Intuitively, the solution to the estimating equations, β̂ M , is the value of the regression parameters β M that provides the closest correspondence between the observed outcomes, Yi , and what is expected under the assumed model, π M ( Xi ). Provided the mean model in Equation 4 is correctly specified, estimating Equations 5 are unbiased (ie, they have zero expectation) regardless of the specific choice of the assumed variance-covariance V ; hence, the corresponding regression parameter estimates β̂ M are consistent (asymptotically unbiased).

Get Radiology Tree app to read full this article<

Interpretation of Regression Parameters

Get Radiology Tree app to read full this article<

βC1=logitπC(Xij,1=1,Xij,2,bi)−logitπC(Xij,1=0,Xij,2,bi). β

logit

(

)

−

logit

(

)

Hence, in addition to holding patient age ( X__ij ,2 ) constant, interpreting the conditional log-odds ratio βC1 β

C requires holding constant, or conditioning on, the value of the radiologist-specific effect, b__i . Consequently, βC1 β

C is referred to as a “conditional” or “cluster-specific” parameter. In contrast, the interpretation of the marginal log-odds ratio, derived via

βM1=logitπM(Xij,1=1,Xij,2)−logitπM(Xij,1=0,Xij,2), β

logit

(

)

−

logit

(

)

does not require conditioning on anything beyond the two measured predictor variables. In particular, the interpretation of the marginal log-odds ratio does not require conditioning on the radiologist-specific effect b__i ; hence, βM1 β

M describes differences in performance between two populations of mammograms, averaging across all radiologists. Consequently, βM1 β

M is referred to as a “population-averaged” or “marginal” parameter. Here, the term “marginal” is a statistical term referring to marginalizing (integrating or averaging) over the distribution of a random variable (in this instance, the random variable is the radiologist-specific effect b ).

Get Radiology Tree app to read full this article<

Connections Between the Two Models

Get Radiology Tree app to read full this article<

πM(Xij)=∫bπC(Xij,b)dG(b). π

(

)

∫

(

)

(

)

In this expression, G ( b ) is the distribution of the random effects across clusters, often taken to be normal with zero mean and a constant variance. Examination of this expression reveals that the marginal mean is equal to the average of the conditional mean, averaging with respect to the distribution of the random effects b .

Get Radiology Tree app to read full this article<

Numerical Differences in Conditional and Marginal Regression Parameters

Get Radiology Tree app to read full this article<

Table 1

Marginal Odds Ratios for Various Values of the Conditional Odds Ratio, the Conditional Intercept (β 0 C ), And Corresponding Mean Response When X = 0 (π 0 C ), and the Standard Deviation (SD) of the Normally Distributed Radiologist-specific Effects

Marginal Odds Ratio, exp( βM1 β

M ) Conditional Odds Ratio, exp( βC1 β

C ) SD for X = 1 SD for X = 0βC0 β

C = −2.2 ( πC0 π

C = .10)βC0 β

C = −1.1 ( πC0 π

C = .25)βC0 β

C = 0 ( πC0 π

C = .50)βC0 β

C = 1.1 ( πC0 π

C = .75)βC0 β

C = 2.2 ( πC0 π

C = .90) 1.00 0.50 0.50 1.00 1.00 1.00 1.00 1.00 1.00 0.79 0.88 1.00 1.13 1.26 2.00 0.48 0.69 1.00 1.45 2.09 1.00 0.50 1.26 1.13 1.00 0.88 0.79 1.00 1.00 1.00 1.00 1.00 1.00 2.00 0.61 0.78 1.00 1.28 1.65 2.00 0.50 2.09 1.45 1.00 0.69 0.48 1.00 1.65 1.28 1.00 0.78 0.61 2.00 1.00 1.00 1.00 1.00 1.00 2.00 0.50 0.50 1.96 1.93 1.93 1.95 1.97 1.00 1.55 1.70 1.93 2.21 2.50 2.00 0.94 1.33 1.93 2.82 4.12 1.00 0.50 2.32 2.03 1.78 1.60 1.48 1.00 1.83 1.79 1.78 1.81 1.88 2.00 1.11 1.40 1.78 2.32 3.10 2.00 0.50 3.26 2.22 1.52 1.06 0.76 1.00 2.57 1.95 1.52 1.21 0.96 2.00 1.56 1.53 1.52 1.54 1.59

Get Radiology Tree app to read full this article<

Implications for Science

Get Radiology Tree app to read full this article<

Additional statistical considerations

Get Radiology Tree app to read full this article<

Sample Size

Get Radiology Tree app to read full this article<

Distributional Assumptions for Cluster-specific Effects

Get Radiology Tree app to read full this article<

logitπC(Xij)=βC0+Xij,1βC1+⋅⋅⋅+Xij,pβCp+σijzj logit

(

)

⋅

logσij(Xij)=α0+Xij,1α1+⋅⋅⋅+Xij,pαp. log

⁡

(

)

⋅

zj∼N(0,1) z

∼

(

)

This model can be fit in SAS using PROC NLMIXED (SAS Institute Inc., Cary, NC).

Get Radiology Tree app to read full this article<

Missing Data

Get Radiology Tree app to read full this article<

Discussion

Recommendations

Get Radiology Tree app to read full this article<

Acknowledgments

Get Radiology Tree app to read full this article<

References

1. Mammography Quality Standards Act of 1992, Pub L No 102–539, as amended by Mammography Quality Standards Reauthorization Act of 1998, Pub L No 105–248.
2. Institute of Medicine: Breast imaging quality standards.2005.National Academies PressWashington, DC
3. Elmore J.G., Miglioretti D.L., Reisch L.M., et. al.: Screening mammograms by community radiologists: variability in false-positive rates. J Natl Cancer Inst 2002; 94: pp. 1373-1380.
4. Barlow W.E., Chi C., Carney P.A., et. al.: Accuracy of screening mammography interpretation by characteristics of radiologists. J Natl Cancer Inst 2004; 96: pp. 1840-1850.
5. Smith-Bindman R., Chu P., Miglioretti D.L., et. al.: Physician predictors of mammographic accuracy. J Natl Cancer Inst 2005; 97: pp. 358-367.
6. Miglioretti D.L., Smith-Bindman R., Abraham L., et. al.: Radiologist characteristics associated with interpretive performance of diagnostic mammography. J Natl Cancer Inst 2007; 99: pp. 1854-1863.
7. Taplin S., Abraham L., Barlow W.E., et. al.: Mammography facility characteristics associated with interpretive accuracy of screening mammography. J Natl Cancer Inst 2008; 100: pp. 876-887.
8. Miglioretti D.L., Heagerty P.J.: Marginal modeling of nonnested multilevel data using standard software. Am J Epidemiol 2007; 165: pp. 453-463.
9. Theberge I., Hebert-Croteau N., Langlois A., Major D., Brisson J.: Volume of screening mammography and performance in the Quebec population-based Breast Cancer Screening Program. CMAJ 2005; 172: pp. 195-199.
10. Kan L., Olivotto I.A., Warren Burhenne L.J., Sickles E.A., Coldman A.J.: Standardized abnormal interpretation and cancer detection ratios to assess reading volume and reader performance in a breast screening program. Radiology 2000; 215: pp. 563-567.
11. Coldman A.J., Major D., Doyle G.P., et. al.: Organized breast screening programs in Canada: effect of radiologist reading volumes on outcomes. Radiology 2006; 238: pp. 809-815.
12. Rickard M., Taylor R., Page A., Estoesta J.: Cancer detection and mammogram volume of radiologists in a population-based screening programme. Breast 2006; 15: pp. 39-43.
13. Ballard-Barbash R., Taplin S.H., Yankaskas B.C., et. al.: Breast Cancer Surveillance Consortium: a national mammography screening and outcomes database. AJR Am J Roentgenol 1997; 169: pp. 1001-1008.
14. Carney P.A., Geller B.M., Moffett H., et. al.: Current medicolegal and confidentiality issues in large, multicenter research programs. Am J Epidemiol 2000; 152: pp. 371-378.
15. American College of Radiology: American College of Radiology (ACR) Breast Imaging Reporting and Data System Atlas (BI-RADS Atlas).2003.American College of RadiologyReston, VA
16. Neuhaus J.M., Kalbfleisch J.D.: Between- and within-cluster covariate effects in the analysis of clustered data. Biometrics 1998; 54: pp. 638-645.
17. Rosenberg R.D., Yankaskas B.C., Abraham L.A., et. al.: Performance benchmarks for screening mammography. Radiology 2006; 241: pp. 55-66.
18. Sickles E.A., Miglioretti D.L., Ballard-Barbash R., et. al.: Performance benchmarks for diagnostic mammography. Radiology 2005; 235: pp. 775-790.
19. Diggle P.J., Heagerty P., Liang K.Y., Zeger S.L.: Analysis of longitudinal data.2002.Oxford University PressNew York
20. Zeger S.L., Liang K.Y., Albert P.S.: Models for longitudinal data: a generalized estimating equation approach. Biometrics 1988; 44: pp. 1049-1060.
21. Neuhaus J.M., Kalbfleisch J.D., Hauck W.W.: A comparison of cluster-specific and population-averaged approaches for analyzing correlated binary data. Int Stat Rev 1991; 59: pp. 25-35.
22. McCullagh P., Nelder J.A.: Generalized Linear Models.2nd ed.1989.Chapman & HallLondon
23. Breslow N.E., Day N.E.: Statistical methods in cancer research, Vol 1: the analysis of case-control studies.1980.International Agency for Research on CancerLondon:pp. 5-338.
24. Obuchowski N.A., Beiden S.V., Berbaum K.S., et. al.: Multireader, multicase receiver operating characteristic analysis: an empirical comparison of five methods. Acad Radiol 2004; 11: pp. 980-995.
25. Liang K.Y., Zeger S.L.: Longitudinal data analysis using generalized linear models. Biometrika 1986; 73: pp. 13-22.
26. Miglioretti D.L., Heagerty P.J.: Marginal modeling of multilevel binary data with time varying covariates. Biostatistics 2004; 5: pp. 381-398.
27. Dorfman D.D., Berbaum K.S., Metz C.E.: Receiver operating characteristic rating analysis. Invest Radiol 1992; 27: pp. 723-731.
28. Dorfman D.D., Berbaum K.S., Lenth R.V., Chen Y.F., Donaghy B.A.: Monte Carlo validation of a multireader method for receiver operating characteristic discrete rating data: factorial experimental design. Acad Radiol 1998; 5: pp. 591-602.
29. Obuchowski N.A., Rockette H.E.: Hypothesis testing of diagnostic accuracy for multiple readers and multiple tests: an ANOVA approach with dependent observations. Commun Stat Simul 1995; 24: pp. 185-308.
30. Obuchowski N.A.: Rejoinder. Acad Radiol 1995; 2: pp. S79-S80.
31. Obuchowski N.A.: Multireader, multimodality receiver operating characteristic curve studies: hypothesis testing and sample size estimation using an analysis of variance approach with dependent observations. Acad Radiol 1995; 2: pp. S22-S29.
32. Song X., Zhou X.H.: A marginal model approach for analysis of multi-reader multi-test receiver operating characteristic (ROC) data. Biostatistics 2005; 6: pp. 303-312.
33. Wang Z., Louis T.A.: Matching conditional and marginal shapes in binary random intercept models using a bridge distribution function. Biometrika 2003; 90: pp. 765-775.
34. Wang Z., Louis T.A.: Marginalized binary mixed-effects models with covariate-dependent random effects and likelihood inference. Biometrics 2004; 60: pp. 884-891.
35. Emrich L.J., Piedmonte M.R.: On some small sample properties of generalized estimating equation estimates for multivariate dichotomous outcomes. J Stat Comput Simul 1992; 41: pp. 19-29.
36. Mancl L.A., DeRouen T.A.: A covariance estimator for GEE with improved small-sample properties. Biometrics 2001; 57: pp. 126-134.
37. Hardin J.: Stata’s implementation of GEE. http://www.stata.com/support/faqs/stat/gee.html Accessed August 14, 2008.
38. Hoffman E.B., Sen P.K., Weinberg C.R.: Within-cluster resampling. Biometrika 2001; 88: pp. 1121-1134.
39. Williamson J.M., Datta S., Satten G.A.: Marginal analyses of clustered data when cluster size is informative. Biometrics 2003; 59: pp. 36-42.
40. Neuhaus J.M., McCulloch C.E.: Separating between- and within-cluster covariate effects by using conditional and partitioning methods. J R Statist Soc B 2006; 68: pp. 859-872.
41. Heagerty P.J., Kurland B.F.: Misspecified maximum likelihood estimates and generalised linear mixed models. Biometrika 2001; 88: pp. 973-985.
42. Little J.A., Rubin D.B.: Statistical analysis with missing data.1987.John WileyNew York
43. Laird N.M.: Missing data in longitudinal studies. Stat Med 1988; 7: pp. 305-315.
44. Robins J., Rotnitzky A., Zhao L.P.: Analysis of semi-parametric regression models for repeated outcomes in the presence of missing data. J Am Stat Assoc 1995; 90: pp. 106-121.
45. Rathouz P.: Fixed effects models for longitudinal binary data with drop-outs missing at random. Statistica Sinica 2004; 14: pp. 969-988.
46. Greenland S., Pearl J., Robins J.M.: Confounding and collapsibility in causal inference. Stat Sci 1999; 14: pp. 29-46.
47. Sickles E.A., Wolverton D.E., Dee K.E.: Performance parameters for screening and diagnostic mammography: specialist and general radiologists. Radiology 2002; 224: pp. 861-869.
48. Leung J.W., Margolin F.R., Dee K.E., et. al.: Performance parameters for screening and diagnostic mammography in a community practice: are there differences between specialists and general radiologists?. AJR Am J Roentgenol 2007; 188: pp. 236-241.
49. Heagerty P.J.: Marginally specified logistic-normal models for longitudinal binary data. Biometrics 1999; 55: pp. 688-698.
50. Heagerty P.J., Zeger S.L.: Marginalized multilevel models and likelihood inference. Stat Sci 2000; 15: pp. 1-26.

Statistical Approaches for Modeling Radiologists' Interpretive Performance

Design considerations

Choice of Outcome

Choice of Predictor

Separation of Between-cluster and Within-cluster Predictor Effects

Regression approaches for clustered data

Conditional or Cluster-specific Models

Marginal or Population-averaged Models

Interpretation of Regression Parameters

Connections Between the Two Models

Numerical Differences in Conditional and Marginal Regression Parameters

Implications for Science

Additional statistical considerations

Sample Size

Distributional Assumptions for Cluster-specific Effects

Missing Data

Discussion

Recommendations

Acknowledgments

References

Further Reading

4-D Imaging in Cerebrovascular Disorders by Using 320-Slice CT

Abstracts of Funded National Institutes of Health Grants

Breaking Bad News in the Breast Imaging Setting