The Role of Collateral Paths in Long-range Diffusion of3 He in Lungs

Rationale and Objectives

The hyperpolarized 3 He long-range diffusion coefficient (LRDC) in lungs is sensitive to changes in lung structure due to emphysema, reflecting the increase in collateral paths resulting from tissue destruction. However, no clear understanding of LRDC in healthy lungs has emerged. Here we compare LRDC measured in healthy lungs with computer simulations of diffusion along the airway tree with no collateral connections.

Materials and Methods

Computer simulations of diffusion of spatially modulated spin magnetization were performed in computer-generated, symmetric-branching models of lungs and compared with existing LRDC measurements in canine and human lungs.

Results

The simulations predict LRDC values of order 0.001 cm 2 /sec, approximately 20 times smaller than the measured LRDC. We consider and rule out possible mechanisms for LRDC not included in the simulations: incomplete breath hold, cardiac motion, and passage of dissolved 3 He through airway walls. However, a very low density of small (micron) holes in the airways is shown to account for the observed LRDC.

Conclusion

It is proposed that LRDC in healthy lungs is determined by small collateral pathways.

The advent of technology for the production of approximately liter quantities of hyperpolarized 3 He gas allows imaging of the air spaces of lungs. The first use of the technology was to produce ventilation images ( ) that display the distribution of a single bolus of inhaled 3 He at breath hold. Subsequently, dynamic 3 He MRI was used to show the time evolution of gas distribution, with sub-second time resolution ( ). A quantitative method for measurement of the local fractional ventilation (the fraction of gas replaced with each breath) has also appeared ( ). The local oxygen concentration and its decrease during breath hold have been determined ( ) from the 3 He T 1 , allowing the local ventilation–perfusion ratio to be calculated ( ).

The microstructure of the lung (the acinar airways and alveolar walls) restricts the diffusion of 3 He. In emphysema, expansion of the acinar airways and tissue destruction result in less restriction and larger apparent diffusion coefficient (ADC). Measurements of the ADC are commonly performed ( ) with two b-values, one of which is zero, with bipolar diffusion-sensitizing gradient pulses of 2- to 5-millisecond duration (here b is the weighting of the diffusion-sensitizing gradient pulses). For these times, the 3 He free diffusivity D 0 (in N 2 or air) of about 0.88 cm 2 /sec corresponds to RMS displacements of about 0.7 mm, large enough to thoroughly explore the interior of a typical acinar airway. Measured ADC values in normal human lungs are approximately 0.2 cm 2 /sec and increase in emphysema; in severely diseased lungs, 0.6 cm 2 /sec is common ( ). Likewise, increases of ADC in rats are observed in emphysema ( ). 3 He ADC measurements have yet to enter common clinical practice, though they are regarded as the emerging new gold standard for characterizing the emphysema-component of COPD. Interest is high in using 3 He ADC for early detection of the disease and for following disease progression in drug treatment trials.

Get Radiology Tree app to read full this article<

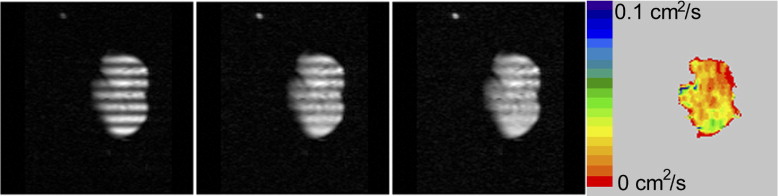
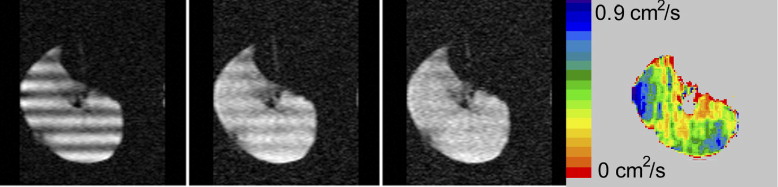
Long-range diffusion

Get Radiology Tree app to read full this article<

S≈exp(−Rt) S

≈

exp

⁡

(

−

)

where

R=(LRDC)k2, R

(

LRDC

)

and k = 2π/λ. The relevant diffusion distance is of order λ/2. The LRDC can also be measured with stimulated echo methods ( ). The underlying physics is the same as the spatially modulated magnetization method, with the initial spin position encoded in the longitudinal magnetization. The primary difference between the methods is whether the modulation is done in the imaging plane or perpendicular to it. The stimulated echo method allows a wide range of modulation wavelengths and diffusion times to be explored ( ).

Get Radiology Tree app to read full this article<

Computer simulations

Get Radiology Tree app to read full this article<

Results

Get Radiology Tree app to read full this article<

Discussion

Get Radiology Tree app to read full this article<

Lack of Breath Hold and Cardiogenic Mixing

Get Radiology Tree app to read full this article<

Permeation Through Airway Walls

Get Radiology Tree app to read full this article<

J→=−D∇C−→−. J

→

−

∇

→

Here the flux is measured in particles (or spins) per time per area and C is in particles (or spins) per volume.

Get Radiology Tree app to read full this article<

J=−DWsC2−sC1x. J

−

Get Radiology Tree app to read full this article<

J=−(LRDC)C2−C1L. J

−

(

)

−

Equating the two expression for the flux J, we obtain

LRDC=DWsL/x. L

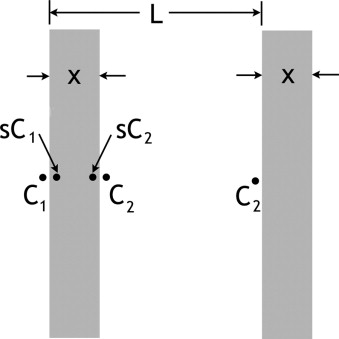
This result is correct when the LRDC so determined is much smaller than the gas free diffusion, D 0 . Using the above values of D W and s and setting L = 600 μm and x = 6 μm, reasonable estimates for acinar airways ( ), we obtain LRDC = 10 −4 cm 2 /sec. This is much smaller than the observed values of LRDC and even much smaller than the computer simulated results. We note that the gas-phase diffusivity is not infinite, which will make the overall diffusivity LRDC only (slightly) smaller. In the same way, lack of equilibrium of the concentration at the gas-liquid surfaces will also reduce LRDC. Overall, the diffusion through the structure of Figure 3 can be regarded as several processes in series, so the overall diffusivity is no larger than the result of Equation 6 . We conclude that this mechanism is negligible, as a result of the low solubility of 3 He in water and its slow diffusion in water. We note that Equation 6 was derived using a linear concentration (or spin magnetization) variation along x , but the result is fully general for length scales longer than L.

Get Radiology Tree app to read full this article<

Diffusion Through Holes

Get Radiology Tree app to read full this article<

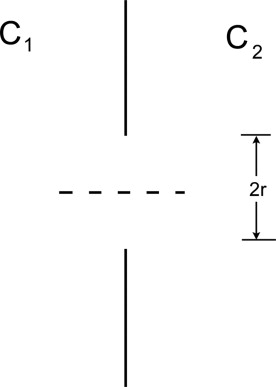
I=DOC2−C12rπr2=DO(C2−C1)rπ/2; I

−

(

−

)

;

here, D 0 is the free diffusivity of the gas. This result, aside from the numerical factor (which is only approximate), can be obtained by dimensional analysis.

Get Radiology Tree app to read full this article<

Conductance=currentpotential difference=2σr Conductance

current

potential difference

This result is obtainable from the electrostatic capacitance CA of a conducting disk relative to a (grounded) surrounding conductor at infinity. The result is given by Smythe ( ) as CA = 8ε 0 r, where ε 0 is the permittivity of free space. Thus, the capacitance to top or bottom alone is 4ε 0 r; the electrostatic and electrical conduction equations are analogous upon substituting the electrostatic ε 0 for the electrical conductivity σ. We note that the two electrical conductances of 4σr in series form a single, net conductance of 2σr. In terms of diffusion, the diffusive conductance of the hole is therefore correctly given by

conductance=IC2−C1=2D0r, conductance

−

which differs numerically only slightly from the simple estimate of Equation 7 . This result has been confirmed by numerical solution of ∇ 2 c = 0. The result also appears in Berg ( ).

Get Radiology Tree app to read full this article<

J¯¯=currentA=NA2D0r(C2−C1). J

(

−

)

Viewed overall, J¯¯ J

¯ can be expressed in terms of the overall diffusivity LRDC and the overall concentration gradient (C 2 − C 1 )/L,

J¯¯=LRDC(C2−C1)/L, J

(

−

)

giving

LRDC=2nD0rL, L

where n is the number density of holes, n = N/A.

Get Radiology Tree app to read full this article<

Conclusions

Get Radiology Tree app to read full this article<

Acknowledgments

Get Radiology Tree app to read full this article<

References

1. Möller H.E., Chen X.J., Saam B., et. al.: MRI of the lungs using hyperpolarized noble gases. Magn Reson Med 2002; 47: pp. 1029-1051.
2. Leawoods J.C., Yablonskiy D.A., Saam B.T., Gierada D.S., Conradi M.S.: Hyperpolarized 3 He gas MR imaging. Concepts Magn Reson 2001; 13: pp. 277-293.
3. Hoffman E.A., van Beek E.: Hyperpolarized media MR imaging: Expanding the boundaries?. Acad Radiol 2006; 13: pp. 929-931.
4. Saam B.T., Yablonskiy D.A., Gierada D.S., Conradi M.S.: Rapid imaging of hyperpolarized gas using EPI. Magn Reson Med 1999; 42: pp. 507-514.
5. Salerno M., Altes T.A., Brookeman J.R., de Lange E.E., Mugler J.P.: Dynamic spiral MRI of pulmonary gas flow using hyperpolarized 3 He: Preliminary studies in healthy and diseased lungs. Magn Reson Med 2001; 46: pp. 667-677.
6. Deninger A.J., Mansson S., Petersson J.S., et. al.: Quantitative measurement of regional lung ventilation using 3 He MRI. Magn Reson Med 2002; 48: pp. 223-232.
7. Deninger A.J., Eberle B., Ebert M., et. al.: Quantification of regional intrapulmonary oxygen partial pressure evolution during apnea by 3 He MRI. J Magn Reson 1999; 141: pp. 207-216.
8. Fischer M.C., Kadlecek S., Yu J.S., et. al.: Measurements of regional alveolar oxygen pressure using hyperpolarized He-3 MRI. Acad Radiol 2005; 12: pp. 1430-1439.
9. Rizi R.R., Baumgardner J.E., Ishii M., et. al.: Determination of regional V A /Q by hyperpolarized 3 He MRI. Magn Reson Med 2004; 52: pp. 65-72.
10. Salerno M., de Lange E.E., Altes T.A., Truwit J.D., Brookeman J.R., Mugler J.P.: Emphysema: hyperpolarized helium 3 diffusion MR imaging of the lungs compared with spirometric indexes: Initial experience. Radiology 2002; 222: pp. 252-260.
11. Saam B.T., Yablonskiy D.A., Kodibagkar V.D., et. al.: MR imaging of diffusion of He-3 gas in healthy and diseased lungs. Magn Reson Med 2000; 44: pp. 174-179.
12. Chen X.J., Hedlund L.W., Möller H.E., Chawla S., Maronpot R.R., Johnson G.A.: Detection of emphysema in rat lungs by using magnetic resonance measurements of 3 He diffusion. Proc Natl Acad Sci USA 2000; 97: pp. 11478-11481.
13. Conradi M.S., Yablonskiy D.A., Woods J.C., et. al.: 3 He diffusion MRI of the lung. Acad Radiol 2005; 12: pp. 1406-1413.
14. Peces-Barba G., Ruiz-Cabello J., Cremillieux Y., et. al.: Helium-3 MRI diffusion coefficient: Correlation to morphometry in a model of mild emphysema. Eur Respir J 2003; 22: pp. 14-19.
15. Yablonskiy D.A., Sukstanskii A.L., Leawoods J.C., et. al.: Quantitative in vivo assessment of lung microstructure at the alveolar level with hyperpolarized 3 He diffusion MRI. Proc Natl Acad Sci USA 2002; 99: pp. 3111-3116.
16. Sukstanskii A.L., Conradi M.S., Yablonskiy D.A.: Relationship between 3 He gas ADCs and lung microstructure. Proc Int Soc Magn Reson Med 2007; 15: pp. 1335.
17. Jensen J.H., Helpern J.A., Ramani A., Hanzhang L., Kaczynski K.: Diffusion kurtosis imaging: The quantification of non-Gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med 2005; 53: pp. 1432-1440.
18. Shanbhag D.D., Altes T.A., Miller G.W., Mata J.F., Knight-Scott J.: Q-space analysis of lung morphmetry in vivo with hyperpolarized 3 He spectroscopy. J Magn Reson Imaging 2006; 24: pp. 84-94.
19. Shanbhag D.D., Altes T.A., Mata J.F., Miller G.W., Knight-Scott J.: SNR performance of Q-space formalism and multi-exponential modeling for hyperpolarized 3 He gas diffusion spectroscopy in human lungs. Proc Int Soc Magn Reson Med 2007; 15: pp. 1286.
20. Alex L., Dougherty L.: MR imaging of motion with spatial modulation of magnetization. Radiology 1989; 171: pp. 841-845.
21. Owers-Bradley J.R., Bennattayalah A., Fichele S., et. al.: Diffusion and tagging of hyperpolarized 3 He in the lungs.2002.pp. 2016.
22. Woods J.C., Yablonskiy D.A., Chino K., Tanoli T.S.K., Cooper J.D., Conradi M.S.: Magnetization tagging decay to measure long-range 3 He diffusion in healthy and emphysematous canine lungs. Magn Reson Med 2004; 51: pp. 1002-1008.
23. Woods J.C., Choong C.K., Yablonskiy D.A., et. al.: Long-range diffusion of hyperpolarized 3 He in excised normal and emphysematous human lungs via magnetization tagging. J Appl Physiol 2005; 99: pp. 1992-1997.
24. Wang C., Miller G.W., Altes T.A., de Lange E.E., Cates G.D., Mugler J.P.: Time dependence of 3 He diffusion in the human lung: Measurement in the long-time regime using stimulated echoes. Magn Reson Med 2006; 56: pp. 296-309.
25. Wang C., Miller G.W., Altes T.A., et. al.: Measuring medium and long-time-scale regional 3 He diffusion using stimulated echoes. Proc Int Soc Magn Reson Med 2007; 15: pp. 458.
26. Wang C., Altes T.A., Miller G.W., et. al.: Short-time-scale and long-time-scale 3 He diffusion MRI in emphysema: Which is more sensitive?. Proc Int Soc Magn Reson Med 2007; 15: pp. 941.
27. West J.B.: Respiratory Physiology.1995.Williams & WilkinsBaltimore, MD:pp. 21-30.
28. Menkes H.A., Macklem P.T.: Collateral flow.Fishman A.P.Handbook of Physiology, Section 3: The Respiratory System.1977.American Physiological SocietyBethesda, MD:pp. 337-353.
29. Weibel E.R.: Design of airways and blood vessels considered as branching trees.Crystal R.G.West J.B.Barnes P.J.Weibel E.R.The Lung: Scientific Foundations.1997.Lippincott-RavenPhiladelphia:pp. 1061-1071.
30. Mathews J., Walker R.L.: Mathematical Methods of Physics.1970.WA BenjaminMenlo Park, CA:pp. 217-252.
31. Bartel S.E.T., Haywood S.E., Woods J.C., et. al.: Simulations and measurements of long-range diffusion of gas in lungs. J Appl Physiol 2008; 104: in press
32. Lide D.R.CRC Handbook of Chemistry and Physics.2004.CRC PressBoca Raton, FL:pp. 8-87.
33. Kirchner B., Stubbs J., Marx D.: Fast anomalous diffusion of small hydrophobic species in water. Phys Rev Lett 2002; 89: pp. 215901-215904.
34. Smythe W.R.: Static and Dynamic Electricity.1968.McGraw-HillNew York:pp. 124.
35. Berg H.C.: Random Walks in Biology.1993.Princeton University PressPrinceton, NJ
36. Bastacky J., Goerke J.: Pores of Kohn are filled in normal lungs: Low-temperature scanning electron microscopy. J Appl Physiol 1992; 73: pp. 88-95.
37. Woolcock A.J., Macklem P.T.: Mechanical factors influencing collateral ventilation in human, dog and pig lungs. J Appl Physiol 1971; 30: pp. 99-115.
38. Terry P.B., Traystman R.J., Newball H.H., Batra G., Menkes H.A.: Collateral ventilation in man. N Engl J Med 1978; 298: pp. 10-15.
39. Hogg J.C., Macklem P.T., Thurlbeck W.M.: The resistance of collateral channels in excised human lungs. J Clin Invest 1969; 48: pp. 421-431.
40. Macklem P.T.: Collateral ventilation. N Engl J Med 1978; 298: pp. 49-50.
41. Cetti E.J., Moore A.J., Geddes G.M.: Collateral ventilation. Thorax 2006; 61: pp. 371-373.
42. Inners C.R., Terry P.B., Traystman R.J., Menkes H.A.: Effects of lung volume on collateral and airway resistance in man. J Appl Physiol 1979; 46: pp. 67-73.
43. Kundu P.K., Cohen I.M.: Fluid Mechanics.ed 22002.Academic PressNew York
44. Verbanck S., Paiva M.: Simulation of the apparent diffusion of helium-3 in the human acinus. J Appl Physiol 2007; 103: pp. 249-254.

The Role of Collateral Paths in Long-range Diffusion of3 He in Lungs

Rationale and Objectives

Materials and Methods

Results

Conclusion

Long-range diffusion

Computer simulations

Results

Discussion

Lack of Breath Hold and Cardiogenic Mixing

Permeation Through Airway Walls

Diffusion Through Holes

Conclusions

Acknowledgments

References

Further Reading

A Robust Method for Estimating Regional Pulmonary Parameters in Presence of Noise

Abstracts of Funded National Institutes of Health Grants

Advances in Physiologic, Metabolic, and Molecular Lung Imaging